Apa itu Pertidaksamaan Nilai Mutlak Linear Satu Variabel?
Contoh Soal Pertidaksamaan Nilai Mutlak Linear Satu Variabel Halaman
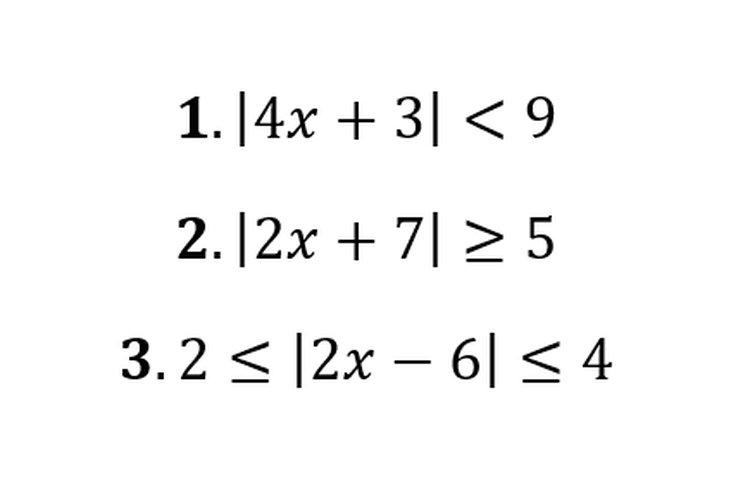
Pertidaksamaan Nilai Mutlak Linear Satu Variabel (Pertidaksamaan Linear) adalah pertidaksamaan dalam bentuk ax+b>c atau ax+b≤c, dimana a dan b adalah konstanta, x adalah variabel, dan c adalah bilangan konstanta.
Mengapa Pertidaksamaan Nilai Mutlak Linear Satu Variabel Penting?
Pertidaksamaan Nilai Mutlak Linear Satu Variabel adalah salah satu konsep yang penting dalam Matematika terutama di jenjang sekolah menengah atas. Salah satu fungsi dari Pertidaksamaan Nilai Mutlak Linear Satu Variabel adalah untuk membantu murid mendalami konsep tentang pertidaksamaan dan membantu dalam persiapan ujian nasional.
Cara Menghitung Pertidaksamaan Nilai Mutlak Linear Satu Variabel
Cara menyelesaikan Pertidaksamaan Nilai Mutlak Linear Satu Variabel adalah dengan membagi persamaan menjadi beberapa kasus berikut:
Kasus 1: Jika (ax+b) ≤ c, maka (ax+b) = c – (-b) ⇃ ax + b ≤ c ⇃ x ≤ &frac(c-b)a
Kasus 2: Jika (ax+b) > c, maka (ax+b) = c + (-b) ⇃ ax + b > c ⇃ x > &frac(c-b)a
Contoh Soal Himpunan Penyelesaian Dari Persamaan Nilai Mutlak

Persamaan Nilai Mutlak adalah persamaan dalam bentuk |ax+b| = c, dimana a dan b adalah konstanta, x adalah variabel, dan c adalah bilangan konstanta.
Cara Menghitung Persamaan Nilai Mutlak
Cara menyelesaikan Persamaan Nilai Mutlak adalah sebagai berikut:
Kasus 1: Jika (ax+b) ≥ 0, maka ax+b = c ⇃ x = &frac(c-b)a
Kasus 2: Jika (ax+b) < 0, maka ax+b = -c ⇃ x < &frac(-c-b)a
Contoh Soal Himpunan Penyelesaian Dari Persamaan Nilai Mutlak
1. Tentukan Himpunan Penyelesaian dari |4x+6| = 10 !
Jawabannya:
|4x+6| = 10 ⇃ 4x+6 = 10 atau 4x+6 = -10
Jadi, Himpunan Penyelesaian dari |4x+6| = 10 adalah x = ½ atau x = -4
2. Tentukan Himpunan Penyelesaian dari |3x+4| > 7 !
Jawabannya:
3x+4 > 7 atau 3x+4 < -7
Jadi, Himpunan Penyelesaian dari |3x+4| > 7 adalah x > 1 atau x < -11/3
Demikianlah penjelasan mengenai Pertidaksamaan Nilai Mutlak Linear Satu Variabel dan Persamaan Nilai Mutlak. Dengan memahami kedua konsep ini, diharapkan siswa dapat memperoleh nilai memuaskan dan lulus ujian dengan baik!





