Apa yang dimaksud dengan pecahan campuran? Pecahan campuran adalah pecahan yang terdiri dari bagian pecahan biasa dan bilangan bulat. Pecahan campuran biasanya digunakan pada kasus-kasus tertentu seperti dalam pengukuran dan operasi kereta api. Berikut ini adalah jawaban untuk beberapa pertanyaan seputar pecahan campuran.
Pecahan Campuran Kelas 5
Mengapa kita perlu memahami pecahan campuran? Pecahan campuran sering digunakan dalam kehidupan sehari-hari dalam pengukuran benda yang tidak bulat seperti kain, kayu, maupun dalam hal perhitungan jarak.
Cara mengubah pecahan campuran menjadi pecahan biasa. Untuk mengubah pecahan campuran menjadi pecahan biasa, kita perlu mengalikan bilangan bulat dengan penyebut pecahan, kemudian tambahkan pembilangnya pada hasil perkalian tersebut.
Contoh: Ubah pecahan campuran 2 1/3 menjadi pecahan biasa.
2 1/3 = (2×3+1)/3 = 7/3
Pecahan Campuran Kelas 6
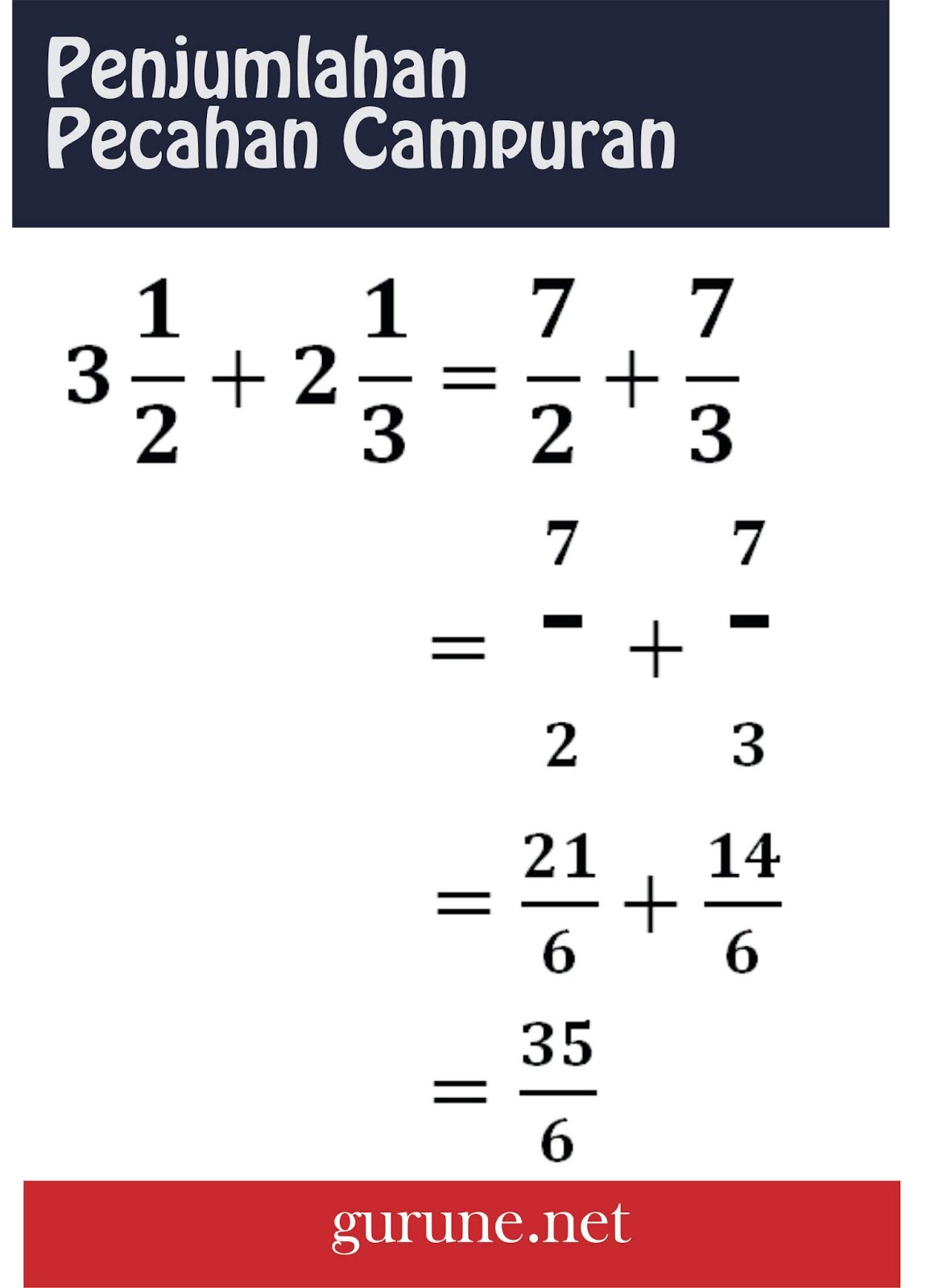
Apa itu pecahan campuran pada kasus pengukuran? Saat mengukur benda-benda takbulat, pecahan biasa tidak lagi digunakan. Sebaliknya, pengukuran dilakukan dalam pecahan campuran. Misalnya, ketika kita membeli kain sepanjang 6 meter 25 centimeter, akan ditulis dalam bentuk pecahan campuran 6 25/100 meter.
Mengapa penggunaan pecahan campuran penting dalam operasi kereta api? Dalam operasi kereta api, stasiun dapat digunakan sebagai acuan jarak antara satu stasiun ke stasiun lainnya. Jarak tersebut dinyatakan dalam bentuk pecahan campuran dan digunakan dalam perhitungan jarak dan kecepatan kereta api. Contohnya, perjalanan kereta api dari Stasiun A ke Stasiun B memiliki jarak sejauh 150 km lebih 132,5 meter, maka jarak tersebut akan ditulis dalam pecahan campuran 150 132,5/1000 km.
Cara menghitung pecahan campuran. Untuk menghitung pecahan campuran, kita perlu mengalikan bilangan bulat dengan penyebut pecahan dan kemudian menambahkan pembilangnya pada hasil perkalian tersebut. Contohnya, jika kita memiliki pecahan campuran 3 2/5, maka untuk mengubahnya menjadi pecahan biasa, kita perlu mengalikan bilangan bulat 3 dengan penyebut pecahan 5 dan tambahkan pembilang 2. Sehingga 3 2/5 = (3×5+2)/5 = 17/5.
Dengan memahami pecahan campuran dan cara-cara menghitungnya, kita dapat dengan mudah menerapkannya dalam kehidupan sehari-hari dan dalam operasi-operasi khusus seperti pengukuran dan operasi kereta api. Semoga informasi ini dapat memberikan manfaat bagi pembaca semua.





