Pasangan Garis yang Sejajar Adalah – Caribes.net
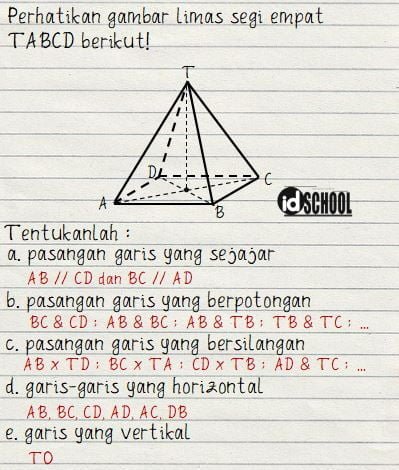
Apa itu pasangan garis yang sejajar?
Pasangan garis yang sejajar adalah dua garis yang tidak pernah bertemu, bahkan jika diperpanjang ke dalam ruang yang tak terbatas. Ini berarti bahwa jika dua garis sejajar ditarik, mereka akan memiliki arah yang sama dan tidak ada titik di mana dua garis tersebut akan bersinggungan. Konsep ini sangat penting dalam matematika dan ilmu lainnya, dan memiliki banyak aplikasi dalam kehidupan sehari-hari.
Persamaan Garis Lurus yang Sejajar dan Tegak Lurus terhadap Suatu Garis
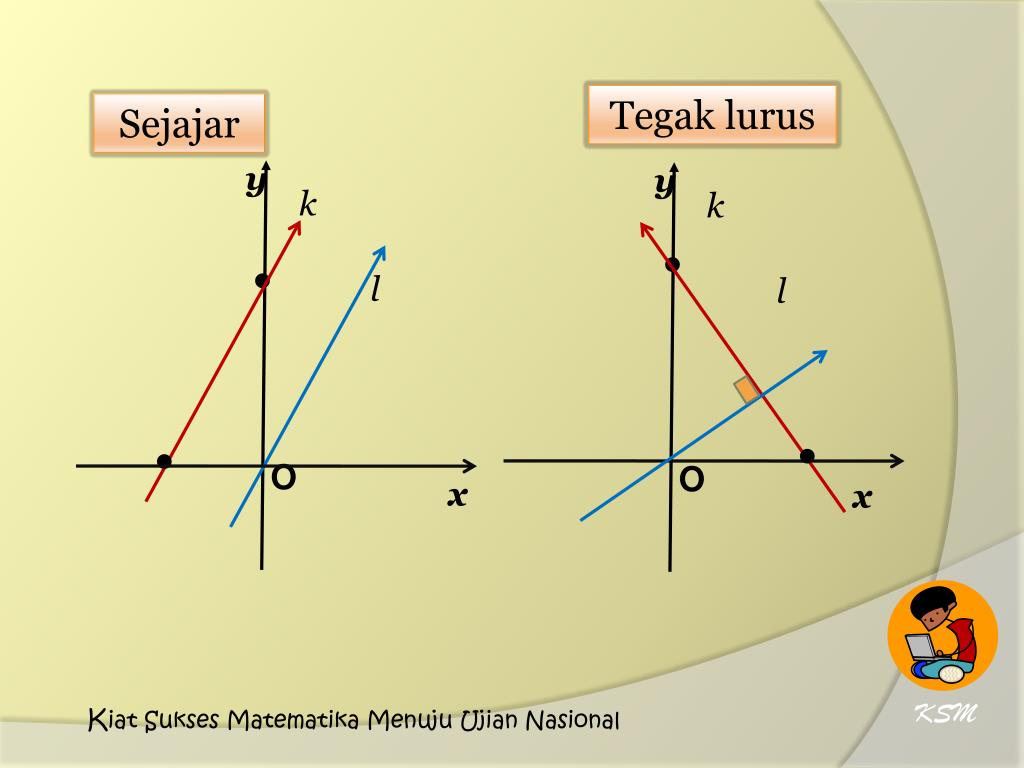
Apa itu persamaan garis lurus yang sejajar dan tegak lurus terhadap suatu garis?
Dalam matematika, garis lurus yang sejajar adalah dua garis lurus yang memiliki gradien atau kemiringan yang sama. Jika dua garis lurus sejajar, maka mereka akan selalu memiliki gradien yang sama, meskipun mungkin memiliki titik awal yang berbeda.
Garis lurus yang tegak lurus terhadap suatu garis adalah garis lurus yang membentuk sudut kanan atau sudut 90 derajat terhadap garis lainnya. Jadi, jika dua garis lurus tegak lurus terhadap garis yang sama, maka mereka akan membentuk sudut kanan satu sama lain.
Persamaan Garis Lurus

Apa itu persamaan garis lurus?
Persamaan garis lurus adalah suatu bentuk persamaan matematika yang digunakan untuk menggambarkan garis lurus di bidang kartesian. Persamaan ini menyatakan hubungan antara variabel x dan y yang menggambarkan koordinat titik-titik pada garis lurus tersebut.
Persamaan garis lurus umumnya ditulis dalam bentuk y = mx + c, di mana m adalah gradien atau kemiringan garis dan c adalah konstanta yang menunjukkan nilai perpotongan garis dengan sumbu y (ketika x = 0).
Pengertian Persamaan Garis Lurus
Persamaan garis lurus adalah suatu bentuk persamaan yang digunakan untuk menggambarkan garis lurus di bidang kartesian. Persamaan ini digunakan untuk menemukan hubungan antara variabel x dan y yang ada pada garis lurus tertentu.
Persamaan garis lurus biasanya ditulis dalam bentuk y = mx + c, di mana m adalah gradien atau kemiringan garis dan c adalah konstanta yang menunjukkan perpotongan garis tersebut dengan sumbu y (ketika x = 0).
Grafik Persamaan Garis Lurus
Salah satu cara untuk menggambarkan persamaan garis lurus adalah dengan menggunakan grafik. Grafik persamaan garis lurus terdiri dari serangkaian titik-titik yang mewakili koordinat x dan y yang memenuhi persamaan tersebut. Setelah titik-titik tersebut dihubungkan, garis lurus dapat terbentuk di bidang kartesian.
Untuk menggambarkan grafik persamaan garis lurus, langkah-langkah berikut dapat diikuti:
- Tentukan dua nilai x yang berbeda-beda.
- Gunakan persamaan garis lurus untuk mencari nilai y yang sesuai dengan setiap nilai x.
- Gunakan pasangan koordinat (x, y) yang didapatkan untuk menggambarkan titik-titik pada bidang kartesian.
- Hubungkan titik-titik tersebut dengan garis lurus.
Rumus Persamaan Garis Lurus
Ada beberapa rumus yang digunakan untuk menemukan persamaan garis lurus, tergantung pada informasi yang diketahui. Beberapa rumus yang umum digunakan dalam persamaan garis lurus adalah:
- Rumus gradien: m = (y2 – y1) / (x2 – x1)
- Rumus titik dan gradien: y – y1 = m(x – x1)
- Rumus dua titik: (y – y1) / (x – x1) = (y2 – y1) / (x2 – x1)
- Rumus gradien dan perpotongan sumbu y: y = mx + c
Contoh Soal Persamaan Garis Lurus
Berikut adalah beberapa contoh soal persamaan garis lurus beserta penyelesaiannya:
Contoh Soal 1:
Tentukan persamaan garis lurus yang melalui titik (2, 3) dan memiliki gradien 4.
Penyelesaian:
Kita dapat menggunakan rumus titik dan gradien y – y1 = m(x – x1) untuk menyelesaikan soal ini. Dalam hal ini, y1 = 3, x1 = 2, dan m = 4.
Jadi, persamaan garis lurus yang melalui titik (2, 3) dan memiliki gradien 4 adalah y – 3 = 4(x – 2).
Contoh Soal 2:
Tentukan persamaan garis lurus yang melalui titik (0, -2) dan (3, 4).
Penyelesaian:
Kita dapat menggunakan rumus dua titik (y – y1) / (x – x1) = (y2 – y1) / (x2 – x1) untuk menyelesaikan soal ini. Dalam hal ini, y1 = -2, x1 = 0, y2 = 4, dan x2 = 3.
Jadi, persamaan garis lurus yang melalui titik (0, -2) dan (3, 4) adalah (y – (-2)) / (x – 0) = (4 – (-2)) / (3 – 0).
Kesimpulan
Pasangan garis yang sejajar adalah dua garis yang tidak pernah bertemu, bahkan jika diperpanjang ke dalam ruang yang tak terbatas. Persamaan garis lurus digunakan untuk menggambarkan garis lurus di bidang kartesian dan menyatakan hubungan antara variabel x dan y pada garis tersebut.
Terdapat beberapa rumus yang dapat digunakan untuk menemukan persamaan garis lurus, termasuk rumus gradien, rumus titik dan gradien, rumus dua titik, dan rumus gradien dan perpotongan sumbu y.
Untuk menggambarkan grafik persamaan garis lurus, langkah-langkah yang dapat diikuti adalah menentukan dua nilai x yang berbeda, mencari nilai y yang sesuai dengan setiap nilai x menggunakan persamaan garis lurus, menggambarkan titik-titik tersebut pada bidang kartesian, dan menghubungkan titik-titik tersebut dengan garis lurus.


