Apa Itu Kubus?
Kubus adalah salah satu bentuk geometri tiga dimensi yang memiliki enam sisi yang berbentuk persegi. Kubus sangat dikenal dan sering digunakan dalam kehidupan sehari-hari, khususnya dalam matematika dan fisika. Bangun ruang ini memiliki banyak sifat dan karakteristik yang menarik untuk dipelajari.
Cara Menghitung Jarak Dua Garis Bersilangan pada Kubus
Jarak antara dua garis bersilangan pada kubus dapat dihitung menggunakan beberapa langkah berikut:
1. Mengidentifikasi Garis Bersilangan
Untuk menghitung jarak antara dua garis bersilangan pada kubus, pertama-tama kita perlu mengidentifikasi garis mana yang bersilangan. Pada kubus, terdapat banyak pasangan garis yang bersilangan. Misalnya, pada kubus ABCD.EFGH, terdapat beberapa pasangan garis yang bersilangan.
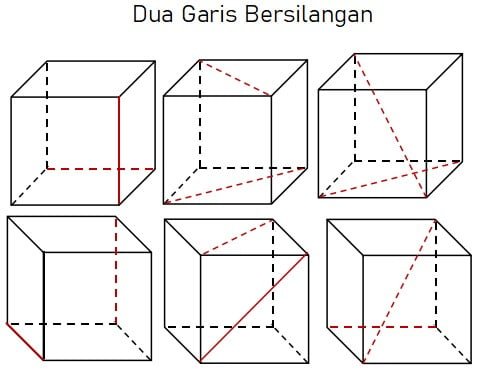
Gambar di atas menunjukkan salah satu contoh pasangan garis yang bersilangan pada kubus ABCD.EFGH. Garis-garis tersebut adalah garis AC dan garis BH. Kedua garis ini saling bersilangan di dalam kubus ABCD.EFGH.
2. Mengukur Jarak Antar Garis Bersilangan
Setelah mengidentifikasi garis bersilangan, langkah selanjutnya adalah mengukur jarak antara dua garis tersebut. Untuk mengukur jarak, kita dapat menggunakan rumus matematika tertentu, yaitu rumus jarak antara dua titik pada koordinat tiga dimensi.
Rumus Jarak Antar Dua Titik pada Koordinat Tiga Dimensi:
Dalam matematika, rumus jarak antara dua titik pada koordinat tiga dimensi dapat dinyatakan sebagai berikut:
√((x2 – x1)^2 + (y2 – y1)^2 + (z2 – z1)^2)
Dalam rumus tersebut, x1, y1, dan z1 adalah koordinat titik pertama, sedangkan x2, y2, dan z2 adalah koordinat titik kedua. Dengan menggunakan rumus ini, kita dapat menghitung jarak antara dua garis bersilangan pada kubus.
Gambaran Bangun Ruang Kubus dengan Garis Bersilangan

Gambar di atas merupakan contoh gambaran bangun ruang kubus dengan garis bersilangan. Pada kubus ABCD.EFGH, terdapat dua pasangan garis yang bersilangan, yaitu garis AC dan garis BD serta garis AB dan garis CD. Garis-garis ini saling bersilangan di dalam kubus ABCD.EFGH.
Contoh Perhitungan Jarak Antar Garis Bersilangan pada Kubus
Berikut ini adalah contoh perhitungan jarak antara dua garis bersilangan pada kubus ABCD.EFGH:
Diketahui koordinat titik A pada kubus ABCD.EFGH adalah (1, 2, 3) dan koordinat titik B adalah (4, 5, 6). Selain itu, koordinat titik C adalah (7, 8, 9) dan koordinat titik D adalah (10, 11, 12).
Perhitungan Jarak Antar Garis AC dan BD:
1. Menghitung jarak antara titik A dan titik C:
√((7 – 1)^2 + (8 – 2)^2 + (9 – 3)^2) = √(36 + 36 + 36) = √108 = 10.39
2. Menghitung jarak antara titik B dan titik D:
√((10 – 4)^2 + (11 – 5)^2 + (12 – 6)^2) = √(36 + 36 + 36) = √108 = 10.39
Jarak antara garis AC dan BD pada kubus ABCD.EFGH adalah 10.39 satuan.
Gambarkan Bangun Ruang Kubus dengan Garis Bersilangan

Gambar di atas merupakan contoh gambaran bangun ruang kubus dengan garis bersilangan. Pada kubus ABCD.EFGH, terdapat beberapa pasangan garis yang bersilangan, seperti garis AC dan garis BD. Garis-garis ini saling bersilangan di dalam kubus ABCD.EFGH.
Kesimpulan
Dalam matematika, kubus adalah salah satu bentuk geometri tiga dimensi yang memiliki enam sisi berbentuk persegi. Kubus memiliki banyak sifat dan karakteristik yang menarik untuk dipelajari, termasuk jarak antara dua garis bersilangan pada kubus.
Untuk menghitung jarak antara dua garis bersilangan pada kubus, pertama-tama kita perlu mengidentifikasi garis mana yang bersilangan. Setelah itu, kita dapat menggunakan rumus jarak antara dua titik pada koordinat tiga dimensi untuk menghitung jarak antara dua garis tersebut. Selanjutnya, kita dapat menggambar bangun ruang kubus dengan garis bersilangan sebagai contoh konkret dari konsep tersebut.
Dengan demikian, pemahaman tentang jarak dua garis bersilangan pada kubus melalui penjelasan, contoh perhitungan, dan gambaran tersebut dapat membantu dalam meningkatkan pemahaman dan menguasai konsep matematika ini.


