Contoh Fungsi Tangga
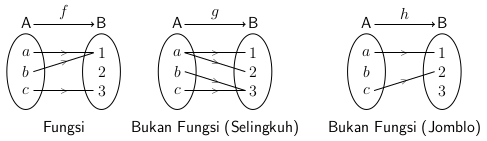
Apa itu fungsi tangga? Fungsi tangga adalah sebuah fungsi matematika yang dapat membuatmu merasa seperti berjalan-jalan di atas tangga. Bayangkan, saat mencoba menginjak langkah pertama, langkah berikutnya akan tersedia di hadapanmu. Begitulah fungsi tangga bekerja, menghubungkan nilai-nilai atau elemen-elemen dalam suatu himpunan secara berurutan.
Soal Diketahui Himpunan Pasangan Berurutan

Apa itu himpunan pasangan berurutan? Himpunan pasangan berurutan adalah suatu himpunan yang berisi pasangan nilai yang diurutkan sesuai dengan aturan tertentu. Setiap pasangan dalam himpunan ini terdiri dari dua nilai yang saling terkait. Misalnya, pasangan (1,2) berarti elemen pertama memiliki nilai 1 dan elemen kedua memiliki nilai 2.
Contoh Soal Himpunan Pasangan Berurutan Yang Merupakan Pemetaan

Apa itu pemetaan? Pemetaan adalah suatu penghubung antara dua himpunan, yaitu himpunan asal (domain) dan himpunan tujuan (range). Setiap elemen dalam himpunan asal dipetakan ke elemen dalam himpunan tujuan. Dalam contoh soal ini, dapat dilihat pemetaan yang terjadi dari himpunan pasangan berurutan (1,x), (2,y), (3,z), (4,a), (5,b) ke himpunan elemen tunggal x, y, z, a, b.
Pengertian Fungsi Tangga dan Himpunan Pasangan Berurutan
Sekarang, sudah ada sedikit gambaran tentang apa itu fungsi tangga dan himpunan pasangan berurutan. Mari kita bahas lebih lanjut tentang definisi, cara kerja, serta proses dan hasil yang dapat diperoleh dari keduanya.
Fungsi Tangga
Fungsi tangga adalah salah satu jenis fungsi matematika yang memetakan himpunan bilangan real ke dalam himpunan bilangan bulat. Namun, jangan khawatir, dalam dunia matematika, fungsi tangga tidak mewajibkanmu untuk naik tangga atau melompat-lompat seperti orang gila.
Jadi, bagaimana cara kerja fungsi tangga? Ketika kita melihat fungsi tangga, seringkali terlihat seperti langkah-langkah dalam sebuah tangga. Setiap langkah tangga merepresentasikan nilai dari himpunan bilangan real. Ketika kita bergerak dari langkah satu ke langkah berikutnya, nilai yang kita dapatkan adalah nilai yang naik secara berturut-turut.
Sebagai contoh, bayangkan sebuah fungsi tangga dengan langkah-langkah sebagai berikut: 1, 2, 3, 4, 5. Saat kita naik tangga ini, setiap langkah memiliki nilai yang lebih besar daripada langkah sebelumnya. Inilah yang menjadi karakteristik utama dari fungsi tangga.
Selain itu, fungsi tangga juga memiliki sifat-sifat tertentu. Pertama, fungsi tangga bersifat deterministik, yang artinya setiap langkah memiliki nilai yang pasti dan saling terkait. Kedua, fungsi tangga bersifat terbatas, artinya terdapat nilai maksimum dan minimum yang dapat dijangkau.
Contoh gambar di atas merupakan salah satu contoh fungsi tangga. Dalam gambar tersebut, terlihat ada sejumlah tangga dengan tinggi yang berbeda-beda. Mari kita amati tangga pertama, dimulai dari langkah 1 dan berakhir pada langkah 5. Setiap langkah pada tangga tersebut memiliki nilai yang lebih besar daripada langkah sebelumnya, sesuai dengan karakteristik dari fungsi tangga.
Himpunan Pasangan Berurutan
Setelah membahas fungsi tangga, sekarang kita beralih ke himpunan pasangan berurutan. Himpunan pasangan berurutan merupakan suatu himpunan yang berisi pasangan nilai yang diurutkan secara teratur berdasarkan aturan tertentu.
Bagaimana cara kerja dan apa definisi dari himpunan pasangan berurutan ini? Seperti namanya, himpunan pasangan berurutan terdiri dari dua nilai yang saling terkait. Biasanya, pasangan ini diatur dalam sepasang kurung , misalnya (1,2), (2,3), (3,4), dan seterusnya.
Dalam dunia matematika, himpunan pasangan berurutan ini sering digunakan untuk memetakan dua himpunan, yaitu himpunan asal (domain) dan himpunan tujuan (range). Setiap anggota dalam himpunan asal dipetakan ke anggota dalam himpunan tujuan. Hal ini berguna untuk menggambarkan hubungan antara dua himpunan tersebut.
Untuk memahami lebih jelas, mari kita lihat contoh soal di atas yang menggambarkan himpunan pasangan berurutan sebagai pemetaan. Terdapat himpunan pasangan berurutan (1,x), (2,y), (3,z), (4,a), (5,b) yang akan dipetakan ke himpunan elemen tunggal x, y, z, a, b.
Dalam contoh soal tersebut, pasangan (1,x) berarti elemen pertama dalam himpunan pasangan berurutan memiliki nilai 1 dan elemen kedua memiliki nilai x. Begitu pula dengan pasangan (2,y), elemen pertama memiliki nilai 2 dan elemen kedua memiliki nilai y, dan seterusnya.
Proses dan Hasil dari Fungsi Tangga dan Himpunan Pasangan Berurutan
Setelah memahami mengenai fungsi tangga dan himpunan pasangan berurutan, mari kita bahas mengenai proses dan hasil yang dapat diperoleh dari keduanya.
Fungsi Tangga
Proses dari fungsi tangga sangat sederhana. Saat kita naik tangga, setiap langkah yang kita ambil memiliki nilai yang lebih besar daripada langkah sebelumnya. Misalnya, jika kita berada pada langkah 1, langkah berikutnya adalah langkah 2 dengan nilai yang lebih besar dari 1. Begitu seterusnya.
Hasil yang dapat diperoleh dari fungsi tangga adalah himpunan nilai yang teratur dan berurutan. Dalam contoh gambar di atas, hasil dari fungsi tangga adalah himpunan langkah pada setiap tangga. Nilai-nilai tersebut dapat dinyatakan dalam bentuk himpunan bilangan, seperti 1, 2, 3, 4, 5 atau himpunan bilangan real di antara 1 dan 5.
Himpunan Pasangan Berurutan
Proses dari himpunan pasangan berurutan adalah mengurutkan pasangan-pasangan nilai sesuai dengan aturan yang ditentukan. Dalam contoh soal di atas, kita memiliki himpunan pasangan berurutan (1,x), (2,y), (3,z), (4,a), (5,b) yang harus diurutkan.
Hasil dari proses ini adalah pemetaan antara himpunan pasangan berurutan dengan himpunan elemen tunggal. Dalam contoh soal tersebut, hasil pemetaan tersebut adalah x, y, z, a, b. Dalam hal ini, x, y, z, a, dan b mewakili nilai dari elemen kedua setiap pasangan dalam himpunan pasangan berurutan.
Contoh dan Kesimpulan
Sekarang, mari kita lihat contoh-contoh lain mengenai fungsi tangga dan himpunan pasangan berurutan, serta kesimpulan yang dapat kita tarik dari pembahasan ini.
Contoh Fungsi Tangga
Berikut adalah contoh-contoh lain dari fungsi tangga yang dapat kita temui dalam kehidupan sehari-hari:
- Menara Eiffel di Paris memiliki langkah-langkah yang membentuk fungsi tangga. Saat kita naik ke atas menara, setiap langkah yang kita ambil memiliki tinggi yang lebih tinggi.
- Anak-anak seringkali menggunakan pijakan tangga saat bermain permainan lompat tali. Setiap pijakan tersebut mewakili langkah dalam fungsi tangga.
Contoh Himpunan Pasangan Berurutan
Berikut adalah contoh-contoh lain dari himpunan pasangan berurutan yang dapat kita temui dalam kehidupan sehari-hari:
- Daftar buku perpustakaan yang diurutkan berdasarkan nomor urut buku dan judulnya.
- Sistem pemesanan tiket online yang memetakan nomor tempat duduk dengan nama penumpang.
Kesimpulan
Dari pembahasan di atas, dapat disimpulkan bahwa fungsi tangga adalah suatu fungsi matematika yang memetakan himpunan bilangan real ke dalam himpunan bilangan bulat, dengan setiap langkah memiliki nilai yang lebih besar daripada langkah sebelumnya. Sedangkan, himpunan pasangan berurutan adalah suatu himpunan yang berisi pasangan nilai yang diurutkan secara teratur berdasarkan aturan tertentu, biasanya digunakan untuk memetakan dua himpunan.


