Mengenal Standar Deviasi
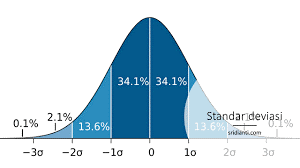
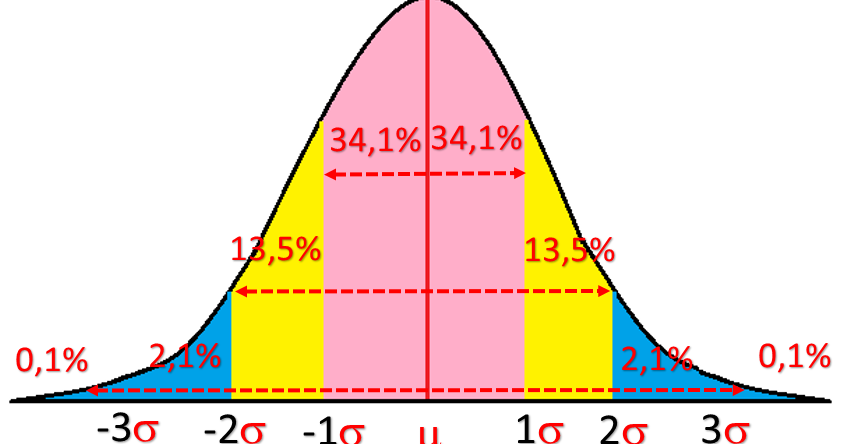
Standar Deviasi merupakan ukuran statistik dari seberapa jauh data dalam kumpulan data tersebar dari nilai rata-rata atau mean. Semakin besar standar deviasi, semakin besar variabilitas atau variasi nilai-nilai dalam kumpulan data. Standar deviasi biasanya digunakan untuk mengetahui seberapa akurat hasil pengujian yang dilakukan.
Mengapa Standar Deviasi Penting?
Standar deviasi penting dalam statistik karena memberikan informasi tentang variabilitas data dalam satu atau lebih sampel. Selain itu, standar deviasi dapat digunakan untuk membuat prediksi dan memperkirakan akurasi dalam satu atau lebih populasi.
Dimana Standar Deviasi Digunakan?
Standar deviasi dapat diterapkan dalam berbagai bidang, seperti keuangan, industri, ilmu sosial, dan lainnya. Misalnya, dalam bidang keuangan, standar deviasi digunakan untuk menemukan risiko investasi. Dalam industri, standar deviasi digunakan untuk mengevaluasi keberhasilan produksi. Dalam ilmu sosial, standar deviasi digunakan untuk memeriksa distribusi data dalam survei atau penelitian.
Kelebihan Standar Deviasi
Kelebihan dari standar deviasi adalah dapat digunakan sebagai alat pengukur variabilitas data. Variabilitas sangat penting dalam statistik karena dapat memberikan gambaran tentang seberapa jauh nilai-nilai dalam kumpulan data tersebar dari rata-rata. Semakin besar nilai standar deviasi, semakin besar range data. Oleh karena itu, standar deviasi dapat digunakan untuk memperkirakan risiko investasi atau membantu dalam pengambilan keputusan.
Kekurangan Standar Deviasi
Kekurangan dari standar deviasi adalah standar deviasi hanya dapat diterapkan pada data numerik. Selain itu, standar deviasi tidak memperhitungkan variasi di luar nilai rata-rata. Hal ini dapat menyebabkan hasil yang tidak akurat jika data yang diamati memiliki distribusi yang tidak normal atau outliers.
Cara Menghitung Standar Deviasi
Cara menghitung standar deviasi adalah sebagai berikut:
- Hitung nilai rata-rata (mean) dari kumpulan data.
- Hitung perbedaan antara setiap data dengan nilai rata-rata.
- Kuadratkan setiap selisih pada langkah 2 dan jumlahkan semua hasilnya
- Bagi jumlah total pada langkah 3 dengan jumlah total data dikurangi 1 dan akar pangkat 2 dari hasilnya.
Contoh Menghitung Standar Deviasi
Misalnya kita memiliki data sebagai berikut: 7, 8, 9, 10, 11. Berikut adalah cara menghitung standar deviasi pada data tersebut.
- Cari nilai rata-rata: (7 + 8 + 9 + 10 + 11) / 5 = 9
- Hitung perbedaan antara setiap data dengan nilai rata-rata:
- (7-9) = -2
- (8-9) = -1
- (9-9) = 0
- (10-9) = 1
- (11-9) = 2
- Kuadratkan setiap selisih dan jumlahkan semua hasilnya: (-2)² + (-1)² + 0² + 1² + 2² = 10
- Bagi jumlah total pada langkah 3 dengan jumlah total data dikurangi 1 dan akar pangkat 2 dari hasilnya:
(10 / (5-1))^(1/2) = 1.58
Jadi, standar deviasi dari data di atas adalah sekitar 1.58.

Cara Menghitung Standar Deviasi pada Excel
Cara mudah untuk menghitung standar deviasi adalah menggunakan perintah STDEV pada Excel. Berikut adalah langkah-langkah untuk menghitung standar deviasi menggunakan Excel.
- Masukkan data pada lembar kerja Excel.
- Pilih sel di mana hasil standar deviasi akan ditampilkan.
- Fungsi STDEV yang sesuai termasuk = STDEV(isi sel range).
- Tekan Enter, dan hasil standar deviasi akan ditampilkan di sel yang dipilih.
Cara ini dapat digunakan untuk setiap jumlah data dan sangat berguna untuk menghitung standar deviasi dari data yang besar.

Cara Menghitung Standar Deviasi pada SPSS
Untuk menghitung standar deviasi pada SPSS, langkah-langkahnya adalah sebagai berikut:
- Buka file data yang akan dihitung standar deviasinya pada SPSS.
- Pilih opsi “Analyze” di menu bar atas.
- Pilih “Descriptive Statistics”, lalu “Descriptives”.
- Pilih variabel yang ingin dihitung standar deviasinya dan pindahkan ke kotak “Variable(s)”
- Klik tombol “Options” dan centang kotak “Standard Deviation”.
- Klik “Continue”, lalu “OK”.
Hasil standar deviasi akan terdapat pada output SPSS.
Kesimpulan
Standar deviasi merupakan ukuran statistik yang penting untuk mengetahui seberapa jauh nilai-nilai dalam kumpulan data tersebar dari rata-rata atau mean. Standar deviasi dapat digunakan dalam berbagai bidang, seperti keuangan, industri, ilmu sosial, dan lainnya. Meskipun standar deviasi memiliki kelebihan dan kekurangan, standar deviasi tetap digunakan sebagai alat pengukur variabilitas dan membantu dalam pengambilan keputusan. Cara memperkirakan standar deviasi melalui perhitungan manual, Excel maupun SPSS dapat digunakan untuk membuat analisis data lebih efektif dan efisien. Semua ini memberikan kesimpulan bahwa standar deviasi memegang peranan penting dalam analisis data.