Garisl tangen pada suatu lingkaran adalah salah satu konsep dasar dalam matematika. Sebagai seorang profesional, kita harus mampu memahami dan menguasai konsep ini untuk meningkatkan kemampuan dalam berpikir logis dan analitis pada setiap situasi yang dihadapi. Pada kesempatan kali ini, kita akan membahas secara detail tentang garis singgung lingkaran.
Gambaran Umum
Garis singgung lingkaran adalah garis yang menyentuh lingkaran pada satu titik saja. Pada titik tersebut, garis singgung tersebut serenjang dengan jari-jari lingkaran. Hal ini bisa dilihat pada gambar di bawah ini:
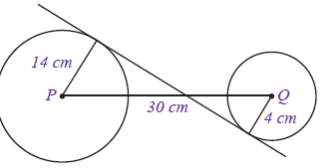
Berdasarkan gambar di atas, dapat kita lihat bahwa garis singgung lingkaran memiliki sifat-sifat khusus, seperti:
- Garis singgung lingkaran akan selalu tegak lurus pada jari-jari lingkaran yang melalui titik yang sama.
- Titik tempat garis singgung dan jari-jari bersentuhan selalu sama.
Apa itu Garis Singgung Lingkaran?
Garis singgung lingkaran adalah suatu garis yang hanya akan bertemu lingkaran pada satu titik saja, yaitu pada titik di mana garis tersebut bersentuhan dengan lingkaran. Sebagai profesional, kita harus mampu mengartikan dan menjelaskan konsep ini secara jelas dan mudah dipahami.
Mengapa Kita Harus Belajar tentang Garis Singgung Lingkaran?
Belajar tentang garis singgung lingkaran penting karena konsep ini sering sekali dipakai dalam matematika, terutama pada materi geometri. Pemahaman yang baik tentang garis singgung lingkaran akan membantu kita dalam menyelesaikan berbagai macam permasalahan dalam matematika secara efektif dan efisien.
Cara Mencari Garis Singgung Lingkaran
Untuk mencari garis singgung lingkaran pada suatu titik, kita harus mengetahui jarak dari titik tersebut ke tengah lingkaran (jari-jari). Berikut adalah langkah-langkah untuk mencari garis singgung lingkaran:
- Tentukan titik pada lingkaran yang ingin kita cari garis singgungnya.
- Hitung jarak dari titik tersebut ke tengah lingkaran.
- Gunakan garis vertical dari titik tersebut untuk membentuk segitiga dengan jari-jari sebagai sisi miring.
- Hitung nilai sudut antara garis vertical tersebut dan jari-jari.
- Hitung nilai tangen dari sudut tersebut.
- Jadikan nilai tangen tersebut sebagai kemiringan garis singgung.
- Gunakan persamaan garis untuk mencari persamaan garis singgung.
Contoh Soal Garis Singgung Lingkaran
Berikut adalah beberapa contoh soal tentang garis singgung lingkaran beserta pembahasannya:
Contoh 1
Diketahui sebuah lingkaran dengan persamaan x2 + y2 = 25. Tentukan persamaan garis singgung pada lingkaran pada titik (3,4).
Jawab:
Pertama-tama, mari kita temukan jari-jari lingkaran ini:
r = √25 = 5
Selanjutnya, kita hitung jarak dari titik (3,4) ke pusat lingkaran:
\Jarak = √[(3-0)2+(4-0)2]
\Jarak = 5
Sekarang, kita gunakan garis vertical dari titik tersebut untuk membentuk segitiga dengan jari-jari sebagai sisi miring:

Hitung nilai sudut antara garis vertical tersebut dan jari-jari:
\Sin(θ) = 4/5
\Sudut = arcsin(4/5)
\Sudut = 53,13°
Hitung nilai tangen dari sudut tersebut:
\Tan(θ) = 0,8
Jadikan nilai tangen tersebut sebagai kemiringan garis singgung:
m = 0,8
Gunakan persamaan garis untuk mencari persamaan garis singgung:
\y – 4 = 0,8(x – 3)
\y – 4 = 0,8x – 2,4
\y = 0,8x + 1,6
Sehingga, persamaan garis singgung pada lingkaran pada titik (3,4) adalah y = 0,8x + 1,6.
Contoh 2
Diketahui sebuah lingkaran dengan pusat titik (5,6) dan jari-jari sepanjang 3. Tentukan persamaan garis singgung pada lingkaran pada titik (8,7).
Jawab:
Hitung jarak dari titik (8,7) ke titik pusat lingkaran:
\Jarak = √[(8-5)2+(7-6)2]
\Jarak = √10
Sekarang, kita gunakan garis vertical dari titik tersebut untuk membentuk segitiga dengan jari-jari sebagai sisi miring:

Hitung nilai sudut antara garis vertical tersebut dan jari-jari:
\Sin(θ) = 1/3
\Sudut = arcsin(1/3)
\Sudut = 19,47°
Hitung nilai tangen dari sudut tersebut:
\Tan(θ) = 0,33
Jadikan nilai tangen tersebut sebagai kemiringan garis singgung:
m = 0,33
Gunakan persamaan garis untuk mencari persamaan garis singgung:
\y – 7 = 0,33(x – 8)
\y – 7 = 0,33x – 2,64
\y = 0,33x + 4,36
Sehingga, persamaan garis singgung pada lingkaran pada titik (8,7) adalah y = 0,33x + 4,36.
Kesimpulan
Sebagai seorang profesional, kita harus memahami dan menguasai konsep dasar matematika seperti garis singgung lingkaran. Menggunakan gambaran umum, penjelasan, cara, dan contoh soal di atas, diharapkan dapat membantu kita dalam memahami konsep garis singgung lingkaran secara lebih baik dan dapat mengaplikasikan konsep ini dalam berbagai macam situasi.




