Pada kesempatan kali ini, kita akan membahas mengenai persamaan dan pertidaksamaan logaritma beserta contoh soalnya. Selain itu, kita juga akan belajar mengenai rumus persamaan kuadrat yang sering kali ditemukan dalam matematika. Simak penjelasan selengkapnya di bawah ini!
Persamaan dan Pertidaksamaan Logaritma
Logaritma merupakan suatu fungsi matematika yang memiliki kebalikan dari eksponen atau pangkat. Dalam logaritma, kita bisa menemukan persamaan dan pertidaksamaan logaritma. Namun sebelum kita membahas mengenai persamaan dan pertidaksamaan logaritma, ada baiknya kita memahami terlebih dahulu apa itu logaritma.
Apa Itu Logaritma?
Logaritma merupakan fungsi matematika yang digunakan untuk menentukan satu bilangan tersebut merupakan pangkat dari bilangan lain. Misalnya, jika ada suatu bilangan x yang merupakan hasil dari pangkat n dengan basis a, maka logaritma dari x dengan basis a dapat dituliskan sebagai:
Jika logaritma dinyatakan dengan simbol log, maka persamaan di atas dapat dituliskan sebagai:
Selain digunakan untuk menentukan pangkat dari suatu bilangan dengan basis tertentu, logaritma juga digunakan untuk menentukan nilai dari suatu bilangan menggunakan basis dan pangkat yang diketahui. Misalnya:
Mengapa Logaritma Penting?
Logaritma memiliki peran penting dalam berbagai bidang, seperti:
- Matematika: Logaritma digunakan sebagai alat untuk menyederhanakan perhitungan matematika yang rumit.
- Sains: Logaritma digunakan dalam berbagai persamaan ilmiah untuk menganalisis data dan menghitung parameter tertentu.
- Teknologi: Logaritma digunakan untuk mempercepat pengolahan data dan membuat algoritma yang lebih efisien.
Cara Menyelesaikan Persamaan dan Pertidaksamaan Logaritma
Untuk menyelesaikan persamaan dan pertidaksamaan logaritma, kita perlu mengikuti beberapa langkah berikut:
- Ubah logaritma menjadi bentuk persamaan kuadrat. Langkah ini dilakukan jika logaritma memiliki pangkat yang lebih dari satu.
- Selesaikan persamaan kuadrat tersebut menggunakan metode faktor, persamaan kuadrat lengkap, atau rumus abc.
- Periksa solusi yang ditemukan. Kita perlu memastikan apakah solusi yang ditemukan sesuai dengan domain dan range dari fungsi logaritma.
Contoh Soal Persamaan dan Pertidaksamaan Logaritma
Berikut adalah contoh soal persamaan dan pertidaksamaan logaritma:
Rumus Persamaan Kuadrat
Selain persamaan dan pertidaksamaan logaritma, rumus persamaan kuadrat juga sering kali ditemukan dalam matematika. Rumus persamaan kuadrat digunakan untuk menemukan akar-akar dari persamaan kuadrat yang berbentuk:
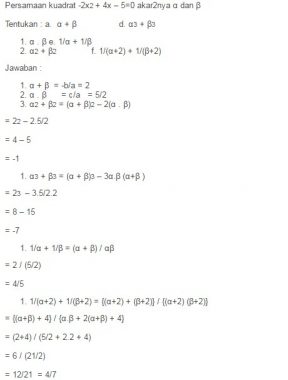
Apa Itu Persamaan Kuadrat?
Persamaan kuadrat merupakan persamaan yang berbentuk:
Di mana a, b, dan c adalah bilangan konstanta yang nilainya bisa positif, negatif, atau nol dan x adalah variabel atau bilangan tak diketahui.
Mengapa Persamaan Kuadrat Penting?
Persamaan kuadrat memiliki peran penting dalam berbagai bidang, seperti:
- Matematika: Persamaan kuadrat digunakan dalam berbagai konsep matematika, seperti fungsi kuadrat dan grafik, dan untuk mempelajari aljabar dasar.
- Fisika: Persamaan kuadrat digunakan untuk menghitung berbagai parameter fisika, seperti jarak, kecepatan, dan percepatan.
- Ekonomi: Persamaan kuadrat digunakan untuk memodelkan dan memprediksi data ekonomi, misalnya dalam penentuan harga dan permintaan barang.
Cara Menyelesaikan Persamaan Kuadrat
Untuk menyelesaikan persamaan kuadrat, kita bisa menggunakan berbagai metode, seperti:
- Metode Faktorisasi: Metode ini dilakukan dengan mencari faktor-faktor dari b dan c sehingga bisa dibuat menjadi bentuk (x-a)(x-b).
- Persamaan Kuadrat Lengkap: Metode ini dilakukan dengan mengubah persamaan kuadrat yang umumnya berbentuk ax^2 + bx + c = 0 menjadi bentuk a(x-h)^2 + k = 0.
- Rumus ABC: Metode ini dilakukan dengan menggunakan rumus x = (-b ± √b^2 – 4ac) / 2a.
Contoh Soal Persamaan Kuadrat
Berikut adalah contoh soal persamaan kuadrat:
Demikianlah penjelasan mengenai persamaan dan pertidaksamaan logaritma beserta contoh soalnya dan rumus persamaan kuadrat beserta contoh soalnya. Semoga penjelasan di atas dapat memperkuat pemahaman Anda dalam matematika. Terima kasih!





