Gambar-gambar di bawah ini akan menunjukkan contoh soal momentum sudut sekaligus menjelaskan apa itu momentum sudut, mengapa penting untuk dipelajari, cara menghitung momentum sudut, serta contoh-contoh sederhana dalam kehidupan sehari-hari.
Contoh Soal Momentum Sudut 1
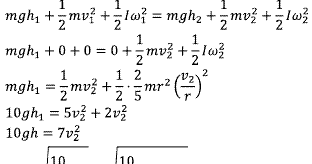
Apa itu momentum sudut? Momentum sudut adalah besaran yang mengukur kuantitas gerakan rotasi suatu benda yang disebabkan oleh besaran gaya yang bekerja pada benda tersebut. Momentum sudut dinyatakan dengan simbol ω dan satuan SI-nya adalah kg*m2/s.
Mengapa momentum sudut penting untuk dipelajari? Momentum sudut sangat penting dalam memahami gerak rotasi benda, khususnya dalam fisika mekanika. Dengan mempelajari momentum sudut, kita dapat menghitung berbagai besaran rotasi benda seperti momen inersia, kecepatan sudut, dan torsi. Dalam aplikasi teknik dan industri, momentum sudut juga penting untuk memahami gerakan mesin, khususnya dalam perancangan dan perhitungan kinerja mesin.
Cara menghitung momentum sudut? Momentum sudut dapat dihitung dengan rumus:
ω = I·α
Dimana ω adalah momentum sudut, I adalah momen inersia suatu benda, dan α adalah percepatan sudut benda.
Contoh Soal Momentum Sudut 2

Contoh di atas menunjukkan dua benda dengan momen inersia m1 dan m2 yang dihubungkan dengan tali. Jika tali ditarik dengan gaya F, tentukan percepatan sudut kedua benda dan momentum sudut keseluruhan sistem.
Contoh di atas dapat diselesaikan dengan menghitung torsi total sistem dan memanfaatkan rumus yang sudah disebutkan sebelumnya:
τ = F·r = I·α
Dengan substitusi momen inersia sebagai berikut:
I = m1·r12 + m2·r22
Didapatkan rumus percepatan sudut:
α = F·(r2-r1)/(m1·r12 + m2·r22)
Sedangkan momentum sudut keseluruhan dapat dihitung dengan:
ω = m1·r12·α + m2·r22·α
Contoh Soal Momentum Sudut 3

Contoh di atas menunjukkan sebuah gantungan yang terdiri dari sebuah benda dengan massa m yang tergantung pada sebuah kawat yang bisa berputar sekitar sumbu tengahnya. Jika benda tersebut dilepaskan dari posisi diam, berapa besar percepatan sudut yang dialami oleh benda di saat jangkar gantungan kembali pada posisi awal?
Contoh di atas dapat diselesaikan dengan menghitung momen inersia dan menerapkan rumus percepatan sudut:
I = 1/2·m·r2
α = -m·g·r/(1/2·m·r2) = -2·g/r
Dimana g adalah gravitasi bumi dan r adalah jarak dari sumbu tengah ke pusat massa benda.
Maka, dengan memasukkan nilai, didapat:
α = -9,8/0,5 = -19,6 rad/s2
Jadi, percepatan sudut yang dialami oleh benda adalah sebesar 19,6 rad/s2.
Contoh Soal Momentum Sudut 4

Contoh di atas menunjukkan sebuah roda yang berputar dengan kecepatan sudut ω. Jika roda tersebut mengalami torsi sebesar τ, berapa besar percepatan sudut yang dialami oleh roda?
Contoh di atas dapat diselesaikan dengan memanfaatkan rumus yang sudah disebutkan sebelumnya:
τ = I·α
Dimana momen inersia untuk roda adalah:
I = 1/2·m·r2
Sehingga:
α = τ/I = τ/(1/2·m·r2)
Jadi, percepatan sudut yang dialami oleh roda adalah sebesar τ/(1/2·m·r2).
Contoh Soal Momentum Sudut 5

Contoh di atas menunjukkan sebuah mobil mainan yang bergerak dengan kecepatan sudut ω. Jika mobil tersebut melintas di atas sebuah permukaan yang tidak rata, berapa besar gaya yang diperlukan agar mobil tetap bergerak dengan kecepatan sudut yang sama?
Contoh di atas dapat diselesaikan dengan memanfaatkan rumus torsi:
τ = F·r
Sedangkan daya yang dihasilkan oleh gaya tersebut diberikan oleh:
P = τ·ω
Sehingga:
F = P/ω·r
Jadi, gaya yang diperlukan agar mobil tetap bergerak dengan kecepatan sudut yang sama adalah sebesar P/ω·r.
Contoh Soal Momentum Sudut 6

Contoh di atas menunjukkan sebuah jarum yang diputar dengan kecepatan sudut ω. Jika ukuran jarum tersebut diperbesar, berapa besar momen inersia yang dialami oleh jarum?
Contoh di atas dapat diselesaikan dengan memanfaatkan rumus momen inersia berikut:
I = 1/2·m·r2
Dengan memperbesar ukuran jarum, maka r-nya akan bertambah besar sehingga momen inersia jarum akan bertambah besar pula.
Contoh Soal Momentum Sudut 7
Contoh di atas menunjukkan sebuah pegas yang terikat pada sebuah benda dengan massa m. Jika benda tersebut diputar searah jarum jam, berapa besar torsi yang dihasilkan oleh pegas tersebut?
Contoh di atas dapat diselesaikan dengan menghitung momen inersia dan menerapkan rumus torsi:
I = 1/2·m·r2
τ = I·α = 1/2·m·r2·α
Sedangkan percepatan sudut dihitung dengan:
α = (2·pi)/T = 2·pi·f
Maka, torsi yang dihasilkan oleh pegas adalah sebesar 1/2·m·r2·(2·pi·f).
Contoh Soal Momentum Sudut 8

Contoh di atas menunjukkan sebuah benda dengan momen inersia I yang melayang di udara. Jika benda tersebut ditarik oleh sebuah tali dengan gaya F, berapa besar kecepatan sudut yang dialami oleh benda tersebut?
Contoh di atas dapat diselesaikan dengan menghitung percepatan sudut dan kecepatan sudut:
I·α = F·r
α = F·r/I
Sedangkan kecepatan sudut dihitung dengan:
ω = α·t
Maka, kecepatan sudut yang dialami oleh benda adalah sebesar F·r/(I·t).
Contoh Soal Momentum Sudut 9

Contoh di atas menunjukkan sebuah meja dengan sebuah bola yang sedang berputar di atas lapangan. Jika lapangan tersebut memiliki koefisien gesekan f, berapa lama waktu yang dibutuhkan bola untuk berhenti berputar?
Contoh di atas dapat diselesaikan dengan memanfaatkan energi kinetik dan energi potensial rotasi:
1/2·I·ω2 = m·g·r·(1-cosθ)
Sehingga:
τ = F·r = I·α
Dimana percepatan sudut bisa dihitung dengan:
α = -τ/I
Akhirnya, waktu yang dibutuhkan untuk bola berhenti berputar adalah:
t = ω/α
Contoh Soal Momentum Sudut 10

Contoh di atas menunjukkan seekor kura-kura dengan momen inersia I sedang berenang di kolam. Jika kura-kura tersebut memutar badannya sebesar θ dengan periode T, berapa magnitude torsi yang dihasilkan oleh kura-kura?
Contoh di atas dapat diselesaikan dengan memanfaatkan rumus momen inersia berikut:
I = m·r2
Sedangkan periode getaran diberikan oleh:
T = 2·pi·sqrt(I·θ/m·g·r2)
Dari rumus periode tersebut, maka magnitude torsi kura-kura bisa dihitung sebagai:
τ = I·(4·pi2·θ)/(T2·g)
Jadi, magnitude torsi yang dihasilkan oleh kura-kura adalah sebesar I·(4·pi2·θ)/(T2·g).





