Hayo, ada yang masih bingung tentang jarak titik ke bidang pada balok? Tenang, kali ini aku akan membahasnya secara lengkap dan mudah dipahami.
Contoh Soal Jarak Titik Ke Bidang Pada Balok
Berikut ini adalah contoh soal mengenai jarak titik ke bidang pada balok:

Nah, gimana? Sudah mampu menyelesaikannya dengan mudah?
Penyelesaian Soal
Untuk menyelesaikan soal tersebut, kita bisa mengikuti langkah-langkah di bawah ini:
Apa itu Jarak Titik Ke Bidang Pada Balok?
Jarak titik ke bidang pada balok adalah jarak terdekat dari suatu titik ke bidang pada permukaan balok.
Mengapa Penting Mengetahui Jarak Titik Ke Bidang Pada Balok?
Dalam matematika, jarak titik ke bidang pada balok sangat penting karena dapat diaplikasikan dalam berbagai bentuk masalah, seperti menghitung jarak antara dua objek atau menentukan letak suatu objek dalam suatu ruangan.
Bagaimana Cara Menghitung Jarak Titik Ke Bidang Pada Balok?
Untuk menghitung jarak titik ke bidang pada balok, kita perlu menggunakan rumus:
d = |ax + by + cz + d| / √(a² + b² + c²)
Dalam rumus di atas, |ax + by + cz + d| adalah jarak titik ke bidang (yang dapat bernilai negatif atau positif), sementara √(a² + b² + c²) membantu menyeimbangkan nilai jarak agar selalu bernilai positif.
Berikut adalah contoh perhitungan jarak titik ke bidang pada balok:
Contoh Soal
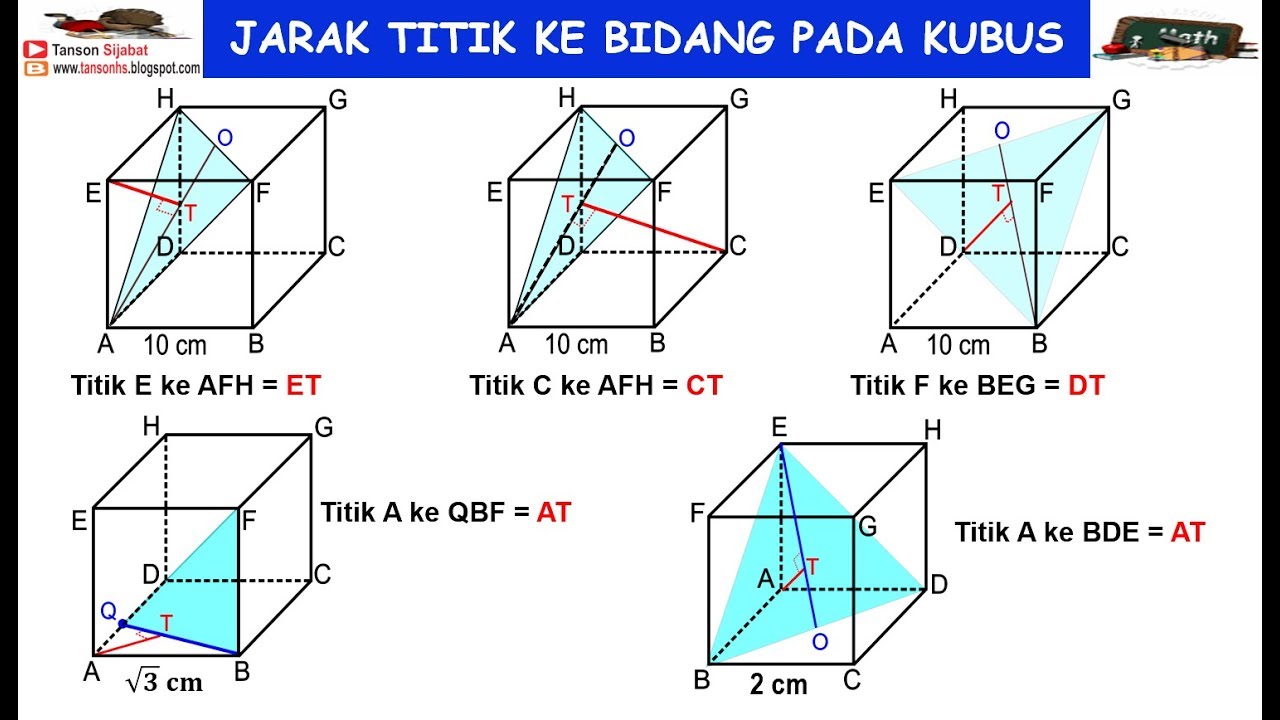
Diketahui balok ABCDEFGH dengan AB = 5, BC = 10, dan CG = 15. Titik P(3, 4, 2) terletak di luar balok dan mempunyai jarak terdekat ke bidang ACE.
Kita perlu menentukan jarak titik P ke bidang ACE.
Penyelesaian
Langkah 1: Tentukan persamaan bidang ACE
Kita dapat menentukan persamaan bidang ACE dengan menggunakan tiga titik yang ada di bidang tersebut. Dalam kasus ini, kita dapat menggunakan titik A(0, 0, 0), titik C(0, 10, 0), dan titik E(5, 10, 0) sehingga diperoleh persamaan:
10y + 5z = 0
Langkah 2: Hitung nilai a, b, dan c
Dari persamaan bidang di atas, kita bisa mengetahui bahwa a = 0, b = 10, dan c = 5.
Langkah 3: Hitung nilai d
Untuk menentukan nilai d, kita dapat menggunakan salah satu titik yang ada di bidang ACE. Kita gunakan titik A(0, 0, 0) sehingga:
d = -(0)(0) + (10)(0) + (5)(0) = 0
Jadi, persamaan bidang ACE adalah 10y + 5z = 0.
Langkah 4: Hitung jarak titik P ke bidang ACE
Untuk menghitung jarak titik P ke bidang ACE, kita dapat menggunakan rumus yang sudah disebutkan di atas:
d = |ax + by + cz + d| / √(a² + b² + c²)
Langkah-langkahnya adalah sebagai berikut:
1. Hitung nilai ax + by + cz + d
Dalam rumus di atas, kita akan menggunakan nilai dari persamaan bidang ACE yang telah kita tentukan sebelumnya.
ax + by + cz + d = 0(3) + 10(4) + 5(2) + 0 = 50
2. Hitung nilai √(a² + b² + c²)
√(a² + b² + c²) = √(0² + 10² + 5²) = √125 ≈ 11,18
3. Hitung nilai d
d = |ax + by + cz + d| / √(a² + b² + c²) = |50| / 11,18 ≈ 4,47
Jadi, jarak terdekat titik P ke bidang ACE adalah sekitar 4,47.
Nah, mudah kan? Jangan lupa latihan terus ya!





