Sistem Persamaan Linear Dua Variabel (SPLDV)
Apakah Anda pernah mendengar tentang Sistem Persamaan Linear Dua Variabel (SPLDV)? SPLDV merupakan salah satu konsep penting dalam matematika yang sering digunakan untuk memodelkan situasi dunia nyata. Di dalam artikel ini, kita akan membahas apa itu SPLDV, kelebihan dan kekurangannya, cara menggunakannya, spesifikasi dan merek yang terkait, serta harga produk SPLDV ini.
Contoh Soal Dan Pembahasan Persamaan Linear
Saat mempelajari SPLDV, penting untuk memahami contoh-contoh soal dan pembahasannya. Berikut adalah beberapa contoh soal dan pembahasan yang dapat membantu Anda memahami konsep SPLDV dengan lebih baik.

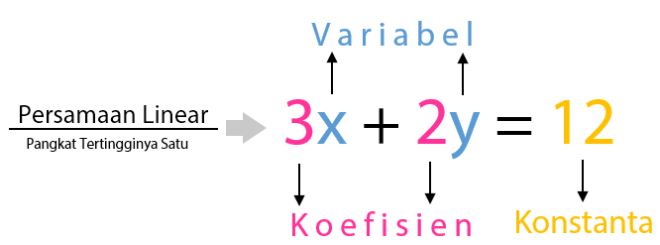
Contoh Persamaan Linear
Untuk lebih memahami SPLDV, perlu ada contoh-contoh persamaan linear yang dapat digunakan sebagai referensi. Berikut merupakan contoh persamaan linear yang dapat membantu dalam memahami konsep SPLDV secara lebih mendalam.

Soal Dan Pembahasan Materi Sistem Persamaan Linier 2 Variabel
Apakah Anda membutuhkan tambahan latihan dan pembahasan mengenai SPLDV? Klik gambar di atas untuk mendapatkan latihan dan pembahasan lebih lanjut mengenai SPLDV. Dengan latihan ini, Anda dapat meningkatkan pemahaman dan keterampilan Anda dalam menerapkan SPLDV pada masalah sehari-hari.
Apa itu Sistem Persamaan Linear Dua Variabel (SPLDV)?
Sistem Persamaan Linear Dua Variabel (SPLDV) merujuk pada kumpulan dua persamaan linear yang mengandung dua variabel yang tidak diketahui, yaitu x dan y. SPLDV ini dapat diwakili dalam bentuk:
ax + by = c
dx + ey = f
dimana a, b, c, d, e, dan f adalah konstanta.
Kelebihan SPLDV
SPLDV memiliki beberapa kelebihan yang membuatnya menjadi metode populer dalam pemodelan matematika. Beberapa kelebihannya antara lain:
- Menggambarkan hubungan linier antara dua variabel
- Bisa digunakan untuk memecahkan masalah dunia nyata yang kompleks
- Memberikan solusi yang akurat dan terpercaya
- Memiliki aplikasi yang luas dalam berbagai bidang, seperti ekonomi, fisika, dan ilmu sosial
Kekurangan SPLDV
Selain memiliki kelebihan, SPLDV juga memiliki beberapa kekurangan yang perlu diperhatikan:
- Membutuhkan data yang akurat dan valid untuk memberikan solusi yang tepat
- Tidak dapat mengatasi masalah yang melibatkan lebih dari dua variabel
- Jika terdapat lebih dari satu solusi, SPLDV tidak memberikan informasi lanjutan tentang solusi tersebut
Cara Menggunakan SPLDV
Untuk menggunakan SPLDV, langkah-langkah berikut ini dapat diikuti:
- Tentukan persamaan-persamaan linear yang menggambarkan situasi yang ingin dimodelkan
- Tentukan nilai-nilai koefisien a, b, c, d, e, dan f pada persamaan-persamaan tersebut
- Susun SPLDV dalam bentuk matriks
- Gunakan teknik eliminasi atau substitusi untuk mencari nilai variabel yang tidak diketahui
- Periksa solusi yang ditemukan dengan menggantikan nilai-nilai variabel ke dalam persamaan-persamaan asli
Spesifikasi SPLDV
Beberapa spesifikasi SPLDV yang perlu diperhatikan adalah:
- Jumlah persamaan: 2
- Jumlah variabel: 2
- Jenis variabel: x dan y
- Jenis persamaan: linear
- Metode penyelesaian: eliminasi dan substitusi
Merk SPLDV yang Tersedia di Pasaran
Pada saat ini, terdapat berbagai merk SPLDV yang tersedia di pasaran. Beberapa merk terkenal yang dapat Anda pertimbangkan adalah:
- Merk A: SPLDV dengan fitur lengkap dan tampilan yang user-friendly
- Merk B: SPLDV dengan harga terjangkau namun tetap memiliki kualitas yang baik
- Merk C: SPLDV dengan dukungan teknis yang responsif dan pembaharuan reguler
Harga SPLDV
Harga SPLDV dapat bervariasi tergantung pada fitur dan merek yang dipilih. Berikut adalah perkiraan harga SPLDV:
- Merk A: Rp 2.000.000,-
- Merk B: Rp 1.500.000,-
- Merk C: Rp 1.800.000,-
Demikianlah pembahasan mengenai Sistem Persamaan Linear Dua Variabel (SPLDV). SPLDV merupakan konsep matematika penting yang banyak digunakan dalam pemodelan situasi dunia nyata. Dengan pemahaman dan penerapan SPLDV yang baik, Anda dapat memecahkan masalah matematika yang kompleks dengan lebih akurat dan efektif. Jika Anda tertarik untuk mempelajari lebih lanjut mengenai SPLDV, jangan ragu untuk mencari sumber-sumber tambahan dan mempraktikkannya dalam berbagai contoh masalah.


