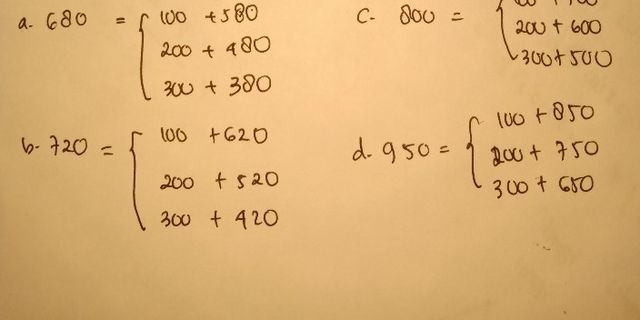Kunci Jawaban Matematika Kelas 4 Halaman 63 Tentukan Pohon Faktor
Apa itu Pohon Faktor?
Pohon Faktor adalah sebuah metode yang digunakan untuk mencari semua faktor dari bilangan tertentu. Dengan menggunakan pohon faktor, kita dapat dengan mudah mengidentifikasi semua pasangan bilangan yang ketika dikalikan menghasilkan bilangan tersebut.
Cara Mencari Pohon Faktor
Untuk mencari pohon faktor, kita perlu mengikuti langkah-langkah berikut:
- Tentukan bilangan yang ingin dicari pohon faktornya.
- Mulailah dengan menempatkan bilangan tersebut pada bagian atas pohon.
- Bagi bilangan tersebut dengan faktor-faktor prima terkecil yang mungkin.
- Tempatkan hasil bagi dan faktor prima sebagai anak-anak dari bilangan di atasnya.
- Lakukan proses pembagian sampai kita tidak bisa lagi mendapatkan faktor prima baru.
- Catat semua bilangan yang berada di bagian bawah pohon faktor sebagai faktor dari bilangan tersebut.
Contoh Pohon Faktor
Sebagai contoh, mari kita tentukan pohon faktor dari bilangan 72.

Langkah 1: Tentukan bilangan 72.
Langkah 2: Tempatkan 72 pada bagian atas pohon faktor.
Langkah 3: Bagi 72 dengan faktor prima terkecil yang mungkin, yaitu 2.
Langkah 4: Tempatkan hasil bagi 36 dan faktor prima 2 sebagai anak-anak dari bilangan di atasnya.
Langkah 5: Bagi 36 dengan faktor prima terkecil yang mungkin, yaitu 2.
Langkah 6: Tempatkan hasil bagi 18 dan faktor prima 2 sebagai anak-anak dari bilangan di atasnya.
Langkah 7: Bagi 18 dengan faktor prima terkecil yang mungkin, yaitu 2.
Langkah 8: Karena 18 tidak dapat dibagi lagi dengan faktor prima 2, kita bagi dengan faktor prima terkecil yang belum pernah kita gunakan sebelumnya, yaitu 3.
Langkah 9: Tempatkan hasil bagi 6 dan faktor prima 3 sebagai anak-anak dari bilangan di atasnya.
Langkah 10: Bagi 6 dengan faktor prima terkecil yang mungkin, yaitu 2.
Langkah 11: Karena 6 tidak dapat dibagi lagi dengan faktor prima 2, kita bagi dengan faktor prima terkecil yang belum pernah kita gunakan sebelumnya, yaitu 3.
Langkah 12: Karena 3 adalah bilangan prima, kita tidak bisa membaginya lagi.
Langkah 13: Catat semua bilangan yang berada di bagian bawah pohon faktor sebagai faktor dari bilangan 72, yaitu 2, 2, 2, 3, dan 3. Jadi, pohon faktor dari bilangan 72 adalah:
2 × 2 × 2 × 3 × 3 = 72
Dengan menggunakan pohon faktor, kita dapat dengan mudah menemukan bahwa pasangan bilangan 2, 2, 2, 3, dan 3, ketika dikalikan menghasilkan bilangan 72.
Kesimpulan
Pohon faktor adalah sebuah metode yang digunakan untuk mencari semua faktor dari bilangan tertentu dengan cara membentuk pohon yang melibatkan pembagian bilangan dengan faktor-faktor primanya. Dengan menggunakan pohon faktor, kita dapat menjawab pertanyaan seperti “Tentukan pohon faktor dari bilangan berikut” dengan mudah dan cepat. Dengan memahami konsep pohon faktor, kita dapat meningkatkan pemahaman kita tentang bilangan dan hubungan antara faktor-faktornya.
Kunjungi juga halaman Kunci Jawaban Matematika Kelas 4 Halaman 63 Tentukan Pohon Faktor untuk melihat contoh pohon faktor dari berbagai bilangan.
Top 10 tuliskan tiga kemungkinan pasangan bilangan dengan jumlah
Apa itu Pasangan Bilangan?
Pasangan bilangan adalah dua bilangan yang dikombinasikan bersama dengan operasi matematika tertentu. Dalam hal ini, kita akan mencari tiga kemungkinan pasangan bilangan dengan jumlah tertentu.
Cara Mencari Tiga Kemungkinan Pasangan Bilangan dengan Jumlah
Untuk mencari tiga kemungkinan pasangan bilangan dengan jumlah tertentu, kita perlu mengikuti langkah-langkah berikut:
- Tentukan jumlah yang diinginkan.
- Gunakan rumus a + b = c, di mana a dan b adalah pasangan bilangan yang ingin kita cari dan c adalah jumlah yang diinginkan.
- Coba semua kombinasi pasangan bilangan yang mungkin dan periksa apakah jumlahnya sama dengan yang diinginkan.
- Catat semua kemungkinan pasangan bilangan yang memenuhi syarat.
Contoh Tiga Kemungkinan Pasangan Bilangan dengan Jumlah
Sebagai contoh, mari kita tuliskan tiga kemungkinan pasangan bilangan dengan jumlah 10.
Langkah 1: Tentukan jumlah 10.
Langkah 2: Gunakan rumus a + b = c.
10 = a + b
Langkah 3: Coba semua kombinasi pasangan bilangan yang mungkin dan periksa apakah jumlahnya sama dengan 10.
Contoh 1: a = 1, b = 9
1 + 9 = 10 (sama dengan 10)
Contoh 2: a = 2, b = 8
2 + 8 = 10 (sama dengan 10)
Contoh 3: a = 3, b = 7
3 + 7 = 10 (sama dengan 10)
Langkah 4: Catat semua kemungkinan pasangan bilangan yang memenuhi syarat. Jadi, tiga kemungkinan pasangan bilangan dengan jumlah 10 adalah (1, 9), (2, 8), dan (3, 7).
Dengan menggunakan langkah-langkah di atas, kita dapat dengan mudah menemukan tiga kemungkinan pasangan bilangan dengan jumlah tertentu.
Kesimpulan
Pasangan bilangan adalah dua bilangan yang dikombinasikan bersama dengan operasi matematika tertentu. Dalam mencari tiga kemungkinan pasangan bilangan dengan jumlah tertentu, kita menggunakan rumus a + b = c dan mencoba semua kombinasi pasangan bilangan yang mungkin. Dengan menggunakan cara ini, kita dapat dengan mudah menemukan semua kemungkinan pasangan bilangan yang memiliki jumlah tertentu.
Kunjungi juga halaman Top 10 tuliskan tiga kemungkinan pasangan bilangan dengan jumlah untuk melihat contoh lebih lanjut tentang cara menemukan tiga kemungkinan pasangan bilangan dengan jumlah tertentu.
Tentukan Tiga Bilangan Ganjil Berurutan Yang Jumlahnya Sama Dengan 315
Apa itu Bilangan Ganjil?
Bilangan ganjil adalah bilangan yang tidak dapat dibagi habis oleh 2. Bilangan ganjil selalu memiliki nilai satuan yang berakhiran dengan angka 1, 3, 5, 7, atau 9.
Cara Menentukan Tiga Bilangan Ganjil Berurutan yang Jumlahnya Sama dengan 315
Untuk menentukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan 315, kita perlu mengikuti langkah-langkah berikut:
- Tentukan jumlah yang diinginkan, dalam hal ini 315.
- Tentukan bilangan ganjil berurutan yang jumlahnya sama dengan jumlah yang diinginkan.
Contoh Tiga Bilangan Ganjil Berurutan yang Jumlahnya Sama dengan 315
Sebagai contoh, mari kita tentukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan 315.

Langkah 1: Tentukan jumlah 315.
Langkah 2: Tentukan bilangan ganjil berurutan yang jumlahnya sama dengan 315.
Angka ganjil berurutan dimulai dari 1, 3, 5, 7, 9, dan seterusnya.
Cari tiga angka ganjil berurutan yang jumlahnya sama dengan 315.
Contoh: 101 + 103 + 111 = 315
Jadi, tiga bilangan ganjil berurutan yang jumlahnya sama dengan 315 adalah 101, 103, dan 111.
Dengan menggunakan langkah-langkah di atas, kita dapat dengan mudah menentukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan jumlah tertentu.
Kesimpulan
Bilangan ganjil adalah bilangan yang tidak dapat dibagi habis oleh 2 dan selalu memiliki angka satuan yang berakhiran dengan angka 1, 3, 5, 7, atau 9. Untuk menentukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan jumlah tertentu, kita dapat mencari kombinasi bilangan ganjil yang memenuhi kriteria tersebut. Dengan menggunakan cara ini, kita dapat dengan mudah menemukan tiga bilangan ganjil berurutan yang jumlahnya sama dengan nilai yang diinginkan.
Kunjungi juga halaman Tentukan Tiga Bilangan Ganjil Berurutan Yang Jumlahnya Sama Dengan 315 untuk melihat contoh lebih lanjut tentang cara menentukan tiga bilangan ganjil berurutan dengan jumlah tertentu.