Banyak aspek yang perlu diperhatikan dalam matematika, terutama dalam pemecahan masalah persamaan garis lurus. Disini kami akan memberikan pembahasan tentang apa itu persamaan garis lurus, mengapa perlu dipelajari dan bagaimana cara menghitungnya. Selain itu, kami juga akan memberikan contoh soal dan penyelesaiannya untuk mempermudah pemahaman.
Apa itu Persamaan Garis Lurus?
Persamaan garis lurus merupakan bentuk persamaan matematika yang paling dasar, yang sering digunakan untuk menyatakan hubungan antara dua variabel dalam bentuk garis lurus. Persamaan ini terdiri dari variabel-variabel seperti x dan y serta suatu konstanta yang disebut dengan koefisien atau bias. Pada kurva linear, setiap titik berada di garis yang sama dengan kemiringan yang sama pula. Dalam formulasi matematis, persamaan ini dapat dicontohkan sebagai berikut:
y = mx +c
Dimana, m adalah kemiringan dan c adalah penentu persilangan sumbu-y (ordinat). Baik m dan c dapat ditentukan dari dua titik yang terletak pada garis lurus.
Mengapa Perlu Dipelajari?
Kemampuan untuk menghitung atau menggunakan persamaan garis lurus menjadi hal yang sangat penting dalam banyak aspek kehidupan sehari-hari. Banyak industri dan sektor ekonomi menggunakan persamaan garis lurus untuk menentukan tren, melakukan prediksi dan menilai kinerja. Selain itu, kemampuan menghitung persamaan garis lurus juga digunakan secara luas dalam bidang akademis seperti matematika, fisika dan ekonomi.
Cara Menghitung Persamaan Garis Lurus
Untuk menghitung persamaan garis lurus, hal utama yang perlu dipahami adalah kemiringan dan penyesuaian sumbu-y. Berikut adalah langkah-langkah untuk menghitung persamaan garis lurus:
- Tentukan dua titik yang terletak pada garis lurus.
- Hitung kemiringan dengan rumus m=(y2-y1)/(x2-x1)
- Tentukan titik potong sumbu-y (c) dengan memasukkan nilai m dan salah satu titik (x,y) dari garis lurus ke dalam rumus y=mx+c dan diatur dalam bentuk y-c=mx.
Contoh Soal dan Penyelesaiannya
Soal 1
Berikut adalah tabel data untuk nilai x dan y:
| x | y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Penyelesaian
Untuk menentukan persamaan garis lurus dari data di atas, kita perlu menghitung kemiringan dan penyesuaian sumbu-y:
m=(y2-y1)/(x2-x1) = (7-5)/(3-2) = 2/1 = 2
Cara menghitung kemiringan yaitu dengan mengambil dua titik (2,5) dan (3,7) maka selisih y (7-5) dibagi dengan selisih x (3-2) yaitu 2/1.
c=y-mx
c=5-(2×1) = 5-2 = 3
Cara menghitung penyesuaian sumbu-y yaitu dengan menggunakan rumus y = mx + c, kemudian memasukkan nilai m dan salah satu titik dan mencari nilai c.
Sehingga persamaan garis lurus untuk tabel data di atas adalah:
y=2x+3
Soal 2
Berikut adalah satu titik dari garis lurus, dan kemiringan:
Titik = (2,5)
Kemiringan = 3
Penyelesaian
Untuk menentukan persamaan garis lurus dari data di atas, kita perlu menghitung penyesuaian sumbu-y (c):
c=y-mx = 5 – (3×2) = -1
Sehingga persamaan garis lurus untuk titik dan kemiringan di atas adalah:
y=3x-1
Kesimpulan
Persamaan garis lurus merupakan persamaan matematika dasar yang sering digunakan dalam memecahkan masalah dalam berbagai aspek kehidupan. Kemampuan yang baik dalam menghitung atau menggunakan persamaan ini akan memberikan keuntungan dalam bidang akademis dan karir.
Dalam menghitung persamaan garis lurus, harus memperhatikan kemiringan dan penyesuaian sumbu-y. Keterampilan dalam menghitung persamaan ini dapat dilakukan dengan latihan dan pemahaman tentang konsep persamaan garis lurus.
Contoh soal seperti yang sudah dijabarkan di atas akan berguna untuk meningkatkan pemahaman konsep dan mencoba menerapkannya dalam pemecahan masalah yang lebih kompleks. Dalam hal ini, Anda dapat menggunakan formula-formula yang dijabarkan di atas sebagai acuan dalam merumuskan persamaan garis lurus pada masalah yang diberikan.
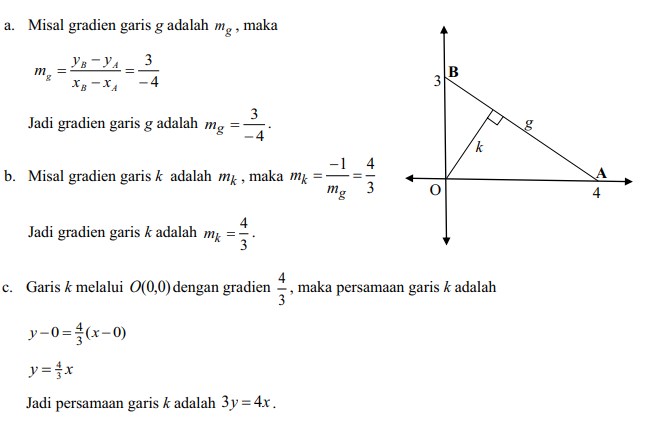
Contoh Soal Grafik Persamaan Garis lurus
Soal 1
Diketahui sebuah garis lurus yang melalui dua titik (4,3) dan (6,5). Tentukan persamaan garis lurus ini!
Penyelesaian
Menggunakan rumus persamaan garis lurus:
m = (y2-y1) / (x2-x1)
m = (5-3) / (6-4) = 2 / 2 = 1
c = y – mx
c = 3 – (1×4) = -1
Sehingga persamaan garis lurusnya adalah:
y = x – 1
Soal 2
Diketahui sebuah garis lurus mempunyai persamaan y = 2x – 3. Tentukan titik potong sumbu-y garis lurus ini!
Penyelesaian
Masukkan titik x = 0 ke dalam persamaan garis lurus:
y = 2(0) – 3 = -3
Sehingga titik potong sumbu-y-nya adalah (-3,0).
Contoh Soal Persamaan Garis Lurus Dan Penyelesaiannya
Soal 1
Diberikan dua titik pada suatu garis lurus yaitu A (2,3) dan B (5,6). Hitunglah persamaan lengkap dari garis lurus yang terjadi dari dua titik tersebut!
Penyelesaian
Yang harus dicari adalah kemiringan m dan konstanta c dari persamaan garis:
m = (y2-y1) / (x2-x1) = (6-3) / (5-2) = 1
c = y – mx = 3 – 1(2) = 1
Sehingga, persamaan lengkap dari garis lurusnya adalah:
y = mx + c = 1x + 1
Soal 2
Sebuah mobil menghabiskan bensin sebanyak 25 liter dalam menempuh jarak 200 km. Jika mobil tersebut memiliki tangki yang dapat menampung bensin sebesar 50 liter, maka berapa kilometer jarak yang dapat ditempuh oleh mobil tersebut?
Penyelesaian
Karena kebutuhan bensin berbanding lurus dengan jarak yang ditempuh, maka dapat digunakan persamaan garis lurus untuk mencari jarak yang dapat ditempuh oleh mobil tersebut:
m = 200/25 = 8
c = 0 (karena mobil harus memiliki bensin untuk dapat digunakan)
Sehingga, persamaan lengkap dari garis lurusnya adalah:
y = mx + c = 8x + 0
Jika mobil memiliki tangki bensin yang dapat menampung 50 liter, maka jarak yang dapat ditempuh adalah:
x = ((50/25)*200)/8 = 25 km
Sehingga jarak yang dapat ditempuh oleh mobil tersebut adalah 25 km.




