Halaman ini akan membahas tentang Besaran Turunan, yaitu besaran fisika yang diperoleh dengan cara membagi sebuah besaran pokok dengan besaran lainnya. Besaran turunan memiliki satuan ukuran yang berbeda dengan besaran pokok, namun tetap berhubungan erat satu sama lain.
Contoh Soal Besaran Turunan
Berikut beberapa contoh soal besaran turunan beserta jawabannya yang bisa membantu Anda dalam memahami konsep ini.

Apa Itu Besaran Turunan?
Besaran turunan adalah besaran fisika yang diperoleh dengan cara membagi sebuah besaran pokok dengan besaran lainnya. Misalnya, kecepatan merupakan besaran turunan dari jarak dibagi waktu, atau percepatan adalah besaran turunan dari kecepatan dibagi waktu.
Mengapa Besaran Turunan Penting?
Besaran turunan sangat penting dalam ilmu fisika dan teknik, karena besaran turunan membantu dalam menggambarkan hubungan antara berbagai besaran fisika yang kompleks dan bervariasi. Misalnya, dalam mekanika, ingin mengetahui kecepatan dan percepatan dari sebuah benda, dapat menghitung dengan mudah karena sudah diketahui dan terhubung dengan besaran turunan.
Cara Menghitung Besaran Turunan
Untuk menghitung besaran turunan, Anda perlu mengetahui rumus dan satuan ukuran dari besaran pokok terlebih dahulu. Kemudian, dapat menghitung besaran turunan dengan cara membagi besaran pokok dengan besaran lainnya.
Contoh Besaran Turunan
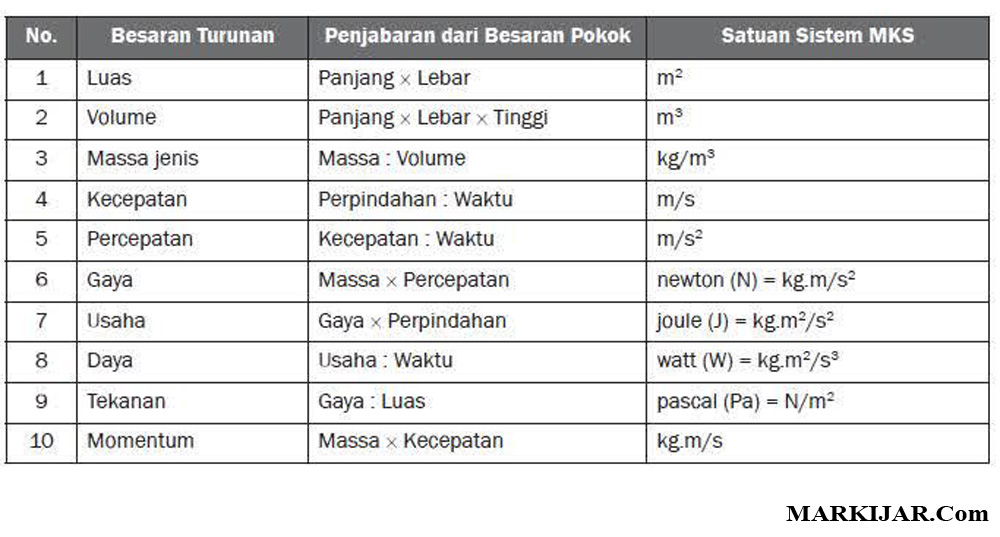
Berikut beberapa contoh besaran turunan:
- Kecepatan adalah besaran turunan dari jarak dibagi waktu
- Percepatan adalah besaran turunan dari kecepatan dibagi waktu
- Tegangan adalah besaran turunan dari gaya dibagi luas
- Jenis daya adalah besaran turunan dari energi dibagi waktu
Contoh Soal Besaran Pokok dan Besaran Turunan Beserta Jawabannya
Berikut beberapa contoh soal besaran pokok dan besaran turunan beserta jawabannya yang bisa membantu Anda dalam memahami konsep ini.
Kesimpulan
Besaran turunan adalah besaran fisika yang diperoleh dengan cara membagi sebuah besaran pokok dengan besaran lainnya. Besaran turunan penting dalam ilmu fisika dan teknik, karena besaran turunan membantu dalam menggambarkan hubungan antara berbagai besaran fisika yang kompleks dan bervariasi. Untuk menghitung besaran turunan, Anda perlu mengetahui rumus dan satuan ukuran dari besaran pokok terlebih dahulu. Contoh soal besaran turunan dan pokok dapat membantu Anda memahami secara praktis tentang konsep ini.





