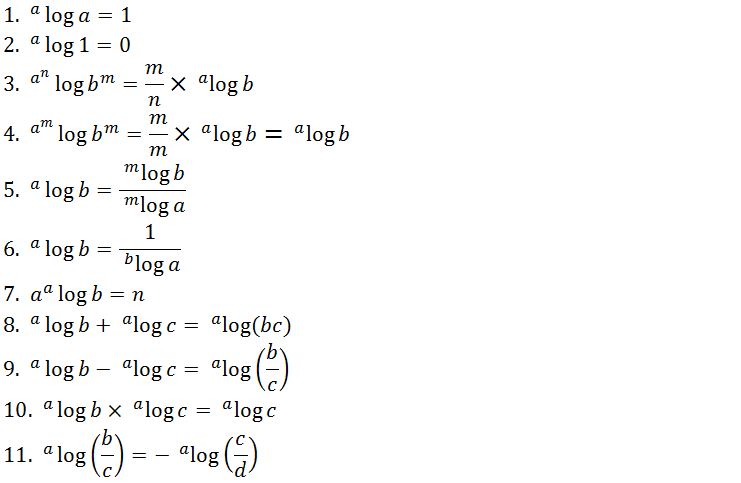Saat ini, logaritma menjadi salah satu topik yang sering dibahas dalam pelajaran matematika, terutama bagi para siswa SMA. Banyak yang mengalami kesulitan dalam memahami konsep logaritma dan cara penyelesaiannya.
Sifat-sifat Logaritma
Sebelum membahas lebih jauh mengenai cara menyelesaikan persamaan logaritma dan contoh soalnya, perlu dipahami terlebih dahulu mengenai sifat-sifat logaritma. Berikut adalah beberapa sifat logaritma yang perlu diketahui:
- Log1 = 0
- Loga a = 1
- Loga xy = Loga x + Loga y
- Loga xⁿ = n Loga x
- Loga (√x) = ½ Loga x
- Loga (1/x) = -Loga x
Persamaan Logaritma dan Cara Penyelesaiannya
Setelah memahami sifat-sifat logaritma, maka kita dapat membahas mengenai cara menyelesaikan persamaan logaritma. Berikut adalah langkah-langkah dalam menyelesaikan persamaan logaritma:
1. Mengidentifikasi Tipe Persamaan Logaritma
Ada beberapa tipe persamaan logaritma yang perlu diketahui, yaitu:
- Loga x = Loga y
- Loga x + Loga y = Loga z
- Loga x – Loga y = Loga z
- Loga x = n
- Loga x = Logb y
2. Menerapkan Sifat-sifat Logaritma
Setelah mengetahui tipe persamaan logaritma, maka langkah selanjutnya adalah menerapkan sifat-sifat logaritma untuk menyelesaikan persamaan. Berikut adalah beberapa contoh penerapan sifat-sifat logaritma:
Contoh Soal
1. Selesaikan Persamaan Logaritma Berikut:
a. Log8 x = 3

Apa itu: Persamaan logaritma dengan bentuk Log8 x = 3
Mengapa: Dalam persamaan ini, kita perlu mencari nilai x dengan basis 8 yang jika di-log-kan akan menghasilkan nilai 3
Cara:
- Terapkan sifat logaritma Loga x = n, maka hasilnya menjadi x = aⁿ
- Ganti bentuk persamaan menjadi x = 8³
- Hasilkan nilai x dengan menghitung 8³ = 512
Jawaban: x = 512
b. 2Log4 x – Log4 y = 3

Apa itu: Persamaan logaritma dengan bentuk 2Log4 x – Log4 y = 3
Mengapa: Dalam persamaan ini, kita perlu mencari nilai x dan y dengan basis 4 dengan cara menggabungkan kedua logaritma yang terpisah
Cara:
- Terapkan sifat logaritma Loga xy = Loga x + Loga y, maka hasilnya menjadi Log4 (x²) – Log4 y = 3
- Terapkan sifat logaritma -Loga x = Loga 1/x, maka hasilnya menjadi Log4 1/yx² = -3
- Hasilkan nilai xy dengan 4⁻³ = 1/64, maka 4⁻³ = 1/(yx²), sehingga 64 = xy²
- Hitung nilai xy dengan akar pangkat dua dari 64, sehingga xy = ±8
Jawaban: x = 2 dan y = 32 atau x = 2 dan y = 1/4
2. Hitung Nilai Logaritma Berikut:
a. Log₃ 27

Apa itu: Nilai logaritma dengan basis 3 dan nilai 27
Mengapa: Dalam persamaan ini, kita perlu mencari nilai logaritma dengan menghitung nilai eksponen yang sanggup memunculkan nilai 27 pada basis 3
Cara: Log₃ 27 = 3 karena 3³ = 27
Jawaban: 3
b. Log₂ 16

Apa itu: Nilai logaritma dengan basis 2 dan nilai 16
Mengapa: Dalam persamaan ini, kita perlu mencari nilai logaritma dengan menghitung nilai eksponen yang sanggup memunculkan nilai 16 pada basis 2
Cara: Log₂ 16 = 4 karena 2⁴ = 16
Jawaban: 4
Demikianlah pembahasan mengenai sifat-sifat logaritma dan cara menyelesaikan persamaan logaritma beserta contoh soalnya. Semoga penjelasan ini dapat membantu memahami konsep logaritma dengan lebih baik dan memberikan kemudahan dalam mengerjakan soal-soal terkait logaritma. Terus belajar dan jangan mudah menyerah!