Contoh Soal Perkalian Skalar Pada Matriks
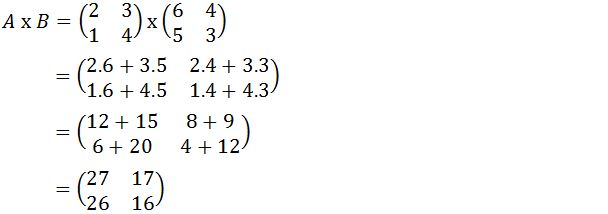
Apa itu Perkalian Skalar Pada Matriks?
Perkalian skalar pada matriks adalah operasi perkalian antara sebuah matriks dan sebuah skalar, dimana setiap elemen matriks dikali dengan skalar tersebut. Hasil perkalian skalar pada matriks adalah sebuah matriks baru yang setiap elemennya diperoleh dengan mengalikan elemen pada matriks awal dengan skalar.
Mengapa Perkalian Skalar Pada Matriks Penting?
Perkalian skalar pada matriks sangat penting dalam komputasi matematika. Dalam bahasa pemrograman, operasi ini sering digunakan untuk mengurangi kebutuhan memori dan untuk meningkatkan performa komputasi matriks. Selain itu, perkalian skalar pada matriks juga sering digunakan dalam pemrosesan gambar, pencitraan medis, dan teknik statistik lainnya.
Bagaimana Cara Melakukan Perkalian Skalar Pada Matriks?
Cara melakukan perkalian skalar pada matriks sangatlah mudah. Anda hanya perlu mengalikan setiap elemen pada matriks dengan skalar tersebut. Berikut adalah contoh cara melakukan perkalian skalar pada matriks:
- Tentukan matriks yang akan dikalikan dengan skalar.
- Tentukan nilai skalar yang akan digunakan untuk perkalian.
- Kalikan setiap elemen pada matriks dengan skalar tersebut.
- Setelah itu, hasil perkalian skalar pada matriks adalah sebuah matriks baru yang terdiri dari elemen-elemen hasil perkalian tersebut.
Contoh Perkalian Skalar Pada Matriks
Berikut adalah contoh perkalian skalar pada matriks:
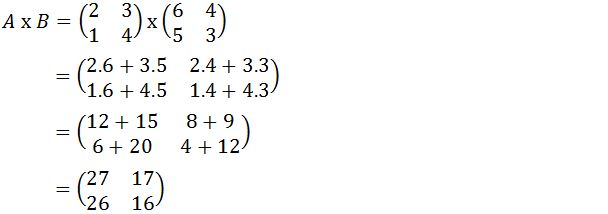
Diketahui matriks A dan skalar x:
A = [2 4 6]
[1 3 5]
[7 9 11]
x = 2
Maka hasil perkalian skalar A dengan x adalah:
A’ = [4 8 12]
[2 6 10]
[14 18 22]
Contoh Perkalian Matriks 3X3

Apa itu Perkalian Matriks 3X3?
Perkalian matriks 3×3 adalah operasi perkalian antara dua matriks yang masing-masing memiliki tiga baris dan tiga kolom. Dalam operasi ini, elemen-elemen dalam baris pertama dari matriks pertama dikalikan dengan elemen-elemen dalam kolom pertama dari matriks kedua. Begitu juga untuk elemen-elemen dalam baris kedua dan ketiga dari matriks pertama dan kolom-kolom kedua dan ketiga dari matriks kedua. Setelah itu, hasil perkalian adalah sebuah matriks 3×3 baru, dimana setiap elemen diperoleh dengan menjumlahkan hasil perkalian antara elemen-elemen tersebut.
Mengapa Perkalian Matriks 3X3 Penting?
Perkalian matriks 3×3 sering digunakan dalam pemrosesan citra, grafika, dan biologi komputasional. Selain itu, operasi ini juga berguna dalam penyelesaian sistem persamaan linear dan kalkulasi prediksi model regresi linear berganda.
Bagaimana Cara Melakukan Perkalian Matriks 3X3?
Cara melakukan perkalian matriks 3×3 adalah sebagai berikut:
- Tentukan dua matriks yang akan dikalikan.
- Periksa apakah jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua. Jika ya, lanjutkan proses perkalian. Jika tidak, operasi perkalian tidak dapat dilakukan.
- Tentukan jumlah kolom dan baris pada matriks hasil. Kedua matriks yang akan dikalikan memiliki tiga baris dan tiga kolom, sehingga hasil perkaliannya juga akan menghasilkan matriks 3×3.
- Kalikan setiap elemen dalam baris pertama pada matriks pertama dengan masing-masing elemen dalam kolom pertama pada matriks kedua. Setelah itu, jumlahkan hasil perkalian tersebut. Masukkan hasil penjumlahan tersebut pada baris pertama dan kolom pertama pada matriks hasil.
- Ulangi langkah keempat untuk setiap kolom pada matriks kedua hingga selesai.
- Ulangi langkah kelima untuk setiap baris pada matriks pertama hingga selesai.
- Setelah seluruh elemen pada matriks hasil terisi, maka hasil perkalian matriks 3×3 adalah matriks tersebut.
Contoh Perkalian Matriks 3X3
Berikut adalah contoh perkalian matriks 3×3:

Diketahui matriks A dan B:
A = [1 0 2]
[0 1 1]
[1 0 0]
B = [1 1 1]
[0 1 0]
[0 1 1]
Maka hasil perkalian matriks A dan B adalah:
C = [1 3 3]
[0 2 1]
[1 1 1]




