Contoh Soal Faktorial dan Pembahasannya
Faktorial merupakan bentuk operasi matematika yang biasanya digunakan pada permutasi dan kombinasi. Faktorial ditandai dengan notasi simbol “!” yang ditempatkan pada sebuah bilangan bulat positif. Berikut adalah contoh soal faktorial beserta pembahasannya.
Apa itu Faktorial?
Faktorial merupakan operasi matematika yang digunakan untuk menghitung jumlah kemungkinan susunan atau urutan yang mungkin terbentuk dari sebuah himpunan.
Mengapa Faktorial Penting?
Faktorial sangat penting diketahui karena sering digunakan dalam perhitungan permutasi dan kombinasi. Dalam matematika, permutasi merupakan pengaturan ulang atau pemilihan k hasil dari n objek dengan pengulangan, sedangkan kombinasi merupakan pemilihan k hasil dari n objek tanpa pengulangan dan tanpa memperhatikan urutannya.
Cara Menghitung Faktorial
Untuk menghitung faktorial suatu bilangan, kita perlu mengalikan bilangan tersebut dengan semua bilangan bulat positif yang lebih kecil daripada itu sendiri, hingga mencapai 1. Secara umum, rumus faktorial dituliskan sebagai berikut:
n! = n x (n-1) x (n-2) x … x 2 x 1
Sebagai contoh, kita akan menghitung 5!.
5! = 5 x 4 x 3 x 2 x 1 = 120
Contoh Soal Faktorial Beserta Pembahasannya
Contoh soal 1: Seorang pemilik toko ingin menata daftar produk-produknya. Produk-produk tersebut terdiri dari 5 jenis dan ia ingin menata produk-produknya dalam bentuk urutan yang berbeda-beda. Berapakah jumlah kemungkinan urutan yang dapat ia susun?
Pembahasan:
Karena ada 5 jenis produk, maka n=5. Kita harus mencari banyaknya kemungkinan urutan yang terbentuk dari 5 jenis produk tersebut. Kita dapat menggunakan rumus permutasi sebagai berikut:
n!/(n-k)!
Dimana n adalah banyaknya jenis produk (5), dan k adalah banyaknya produk yang ingin ditampilkan (5).
Sehingga:
5!/(5-5)! = 5! = 5 x 4 x 3 x 2 x 1 = 120
Maka terdapat 120 kemungkinan urutan yang bisa disusun dari 5 jenis produk tersebut.
Contoh soal 2: Seorang perajin ingin membuat keranjang dari bahan-bahan yang tersedia. Dia memiliki 8 jenis bahan yang dapat dipilih. Berapakah banyaknya kemungkinan variasi keranjang yang dapat dibuat?
Pembahasan:
Karena ada 8 jenis bahan yang tersedia, maka n=8. Kita harus mencari banyaknya variasi keranjang yang dapat dibuat, sehingga tidak memerlukan pengaturan yang berbeda-beda. Kita dapat menggunakan rumus kombinasi sebagai berikut:
n!/k!(n-k)!
Dimana n adalah banyaknya jenis bahan (8), dan k adalah banyaknya bahan yang ingin dipakai (4).
Sehingga:
8!/(4!(8-4)!) = 8!/(4! x 4!) = (8 x 7 x 6 x 5)/(4 x 3 x 2 x 1)= 70
Maka terdapat 70 variasi keranjang yang dapat dibuat dari 8 jenis bahan tersebut.
Soal Faktorial Kelas 12 – Status Apik
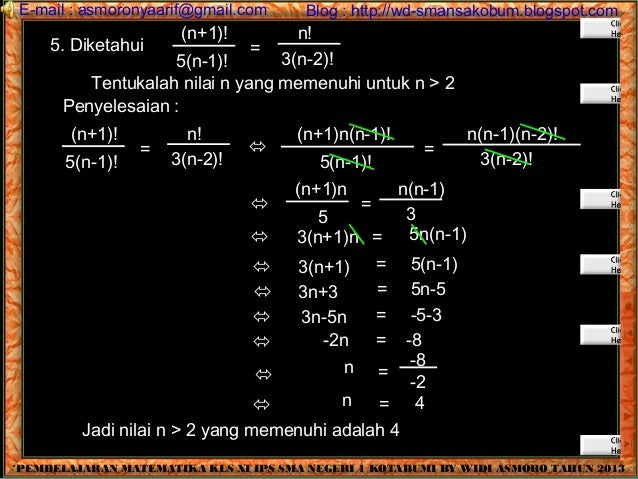
Faktorial adalah bentuk operasi matematika yang sering appear pada soal-soal matematika baik itu di sekolah hingga perkuliahan. Dalam soal-soal tersebut biasanya diberikan variasi soal yang bisa diterapkan dengan menggunakan rumus faktorial. Berikut adalah beberapa contoh soal faktorial kelas 12 beserta pembahasannya.
Apa itu Faktorial?
Faktorial adalah bentuk operasi matematika yang sering muncul dalam soal-soal matematika. Hal ini digunakan untuk menghitung kemungkinan susunan atau urutan yang mungkin terbentuk dari sebuah himpunan.
Mengapa Faktorial Penting?
Faktorial sangat penting diketahui karena sering digunakan untuk perhitungan pada permutasi dan kombinasi matematika. Permutasi adalah pengaturan ulang atau pemilihan hasil dari objek dengan pengulangan, sedangkan kombinasi adalah pemilihan hasil dari objek tanpa pengulangan dan tidak memperhatikan urutannya. Pemahaman faktorial akan memudahkan dalam memahami kedua hal tersebut.
Cara Menghitung Faktorial
Untuk menghitung faktorial suatu bilangan, kita perlu mengalikan bilangan tersebut dengan semua bilangan bulat positif yang lebih kecil daripada itu sendiri, hingga mencapai 1. Secara umum, rumus faktorial dituliskan sebagai berikut:
n! = n x (n-1) x (n-2) x … x 2 x 1
Sebagai contoh, kita akan menghitung 5!.
5! = 5 x 4 x 3 x 2 x 1 = 120
Contoh Soal Faktorial Kelas 12
Contoh soal 1: Ada 5 orang yang akan duduk satu meja mempunyai 5 kursi. Berapa banyak kemungkinan cara menyusun 5 orang tersebut?
Pembahasan:
Kita dapat menggunakan rumus permutasi dalam soal ini, karena urutan dalam penyusunan orang di atas kursi sangat diperhatikan. Kita bisa menghitung berapa banyaknya susunan 5 orang dalam 5 tempat dengan menggunakan rumus:
5! = 5 x 4 x 3 x 2 x 1 = 120
Jadi, ada 120 kemungkinan cara penyusunan 5 orang tersebut.
Contoh soal 2: Terdapat sebuah blok kayu dimana panjang, lebar, dan tingginya masing-masing 4, 6, dan 7 cm. Berapa banyak blok yang dapat tersusun dengan syarat saja sisi-sisinya merepresentasikan satu pemrograman Pyramid yang disebut “M.”?
Pembahasan:
Himpunan dari blok kayu tersebut terdiri dari panjang 4, lebar 6, dan tinggi 7. Ada 3 cara untuk menyusun kayu menjadi blok “M” (persegi panjang dengan ukuran 4 x 6), yaitu dengan posisi kayu panjangnya di atas atau di bawah, dan dengan posisi kayu lebarnya di atas atau di bawah. Kita bisa menggunakan rumus kombinasi untuk menghitung kemungkinan penyusunan kayu tersebut menjadi blok “M” dengan persamaan:
C(3,1) x C(2,1) = 3 x 2 = 6
Jadi, terdapat 6 blok kayu yang dapat tersusun dengan syarat sisi-sisinya merepresentasikan satu pemrograman Pyramid yang disebut “M”.
Contoh soal 3: Di dalam lemari terdapat 5 kaos dan 3 celana. Berapa banyak kaos dan celana yang dapat dipilih jika hanya diambil 4 barang?
Pembahasan:
Kita dapat menggunakan rumus kombinasi dalam soal ini, karena tidak diperhatikan urutan dalam memilih 4 barang. Kita bisa menghitung berapa banyaknya kombinasi 4 barang dari 8 barang untuk memecahkan masalah ini.
C(8,4) = (8!)/(4!(8-4)!) = 70
Jadi, ada 70 cara untuk memilih 4 barang dari 5 kaos dan 3 celana.





