
Contoh Soal Cerita Aplikasi Turunan Fungsi Trigonometri untuk Kamu yang Ingin Menjadi Ahli Matematika
Berikut ini adalah contoh soal cerita aplikasi turunan fungsi trigonometri yang akan membantu kamu memahami konsep turunan fungsi trigonometri.
Apa Itu Fungsi Trigonometri?
Fungsi trigonometri adalah fungsi matematis yang melibatkan sudut dalam penghitungannya. Fungsi ini sangat penting dalam banyak bidang, termasuk matematika, fisika, teknik, dan astronomi. Fungsi trigonometri terdiri dari sine, cosine, tangent, cosecant, secant dan cotangent.
Mengapa Penting untuk Memahami Fungsi Trigonometri?
Memahami fungsi trigonometri sangat penting bagi siapa saja yang ingin menjadi ahli matematika. Fungsi trigonometri merupakan instrumen dasar yang digunakan dalam kebanyakan masalah matematika tingkat lanjut, seperti kalkulus dan statistik.
Cara Menghitung Fungsi Trigonometri
Untuk menghitung fungsi trigonometri, ada beberapa cara yang bisa kamu lakukan, antara lain:
- Memorize nilai-nilai sin, cos, tan, csc, sec, dan cot pada sudut-sudut tertentu;
- Menggunakan kalkulator yang dilengkapi dengan fungsi-fungsi trigonometri;
- Menggunakan rumus yang sesuai dengan permasalahan yang dihadapi.
Contoh Soal Cerita Aplikasi Turunan Fungsi Trigonometri
Berikut ini adalah contoh soal cerita aplikasi turunan fungsi trigonometri:
Sebuah bola dijatuhkan dari ketinggian 80 m. Waktu yang dibutuhkan bola untuk jatuh ke tanah adalah … (dengan memperhitungkan gesekan udara).
Diketahui bahwa w = sin(2θ), di mana θ adalah sudut elevasi bola. Nilai θ yang membuat fungsi w mencapai nilai maksimum adalah … .
Pembahasan Soal Pertama
Soal pertama membutuhkan konsep turunan fungsi sin(θ), di mana θ adalah fungsi waktu. Dari rumus kinematika pada gerak jatuh bebas tanpa hambatan udara, kita dapat menghitung waktu yang dibutuhkan bola untuk jatuh ke tanah sebagai berikut:
s = 1/2 gt²
dengan:
s = jarak yang ditempuh oleh bola
g= percepatan gravitasi (9,8 m/s²)
t = waktu yang dibutuhkan bola untuk jatuh
Pada saat bola terjatuh dari ketinggian 80 m, percepatan gravitasi masih sama, yaitu sebesar 9,8 m/s². Dengan menggunakan rumus di atas, kita dapat menghitung waktu yang dibutuhkan bola untuk jatuh ke tanah seperti berikut:
80 = 1/2 × 9,8 × t²
t = √(80 / (1/2 × 9,8))
t = √(80 / 4,9)
t ≈ 4,04 detik
Pembahasan Soal Kedua
Soal kedua membutuhkan konsep turunan fungsi sin(2θ), di mana θ adalah fungsi elevasi. Maksimum fungsi trigonometri terjadi ketika fungsi tersebut mencapai nilai puncak. Nilai puncak fungsi tersebut dapat ditemukan dengan menghitung turunan pertama dari fungsi tersebut, kemudian mencari titik stasioner dengan cara menyamakan turunan pertama fungsi tersebut dengan nol.
Sebelum kita mencari turunan pertama dari fungsi sin(2θ), kita perlu menggunakan identitas trigonometri untuk mengalihkan fungsi tersebut menjadi fungsi yang lebih mudah diintegrasikan. Identitas yang kita gunakan adalah:
sin(2θ) = 2sinθcosθ
Dalam matematika, ada rumus umum untuk menghitung turunan trigonometri. Rumus tersebut adalah:
d/dθ sin(θ) = cos(θ)
d/dθ cos(θ) = -sin(θ)
Kembali ke masalah yang diberikan, kita dapat menghitung turunan pertama dari w = sin(2θ) dengan menggunakan identitas trigonometri di atas, seperti berikut:
w’ = d/dθ(sine(2θ))
w’ = d/dθ(2sinθcosθ)
w’ = [d/dθ(2sinθ)]cosθ + sinθ[d/dθ(cosθ)]
w’ = (2cosθ)cosθ + sinθ(-sinθ) (d/dθ sin(θ) = cos(θ) dan d/dθ cos(θ) = -sin(θ))
w’ = 2cos²θ – sin²θ
Setelah menemukan turunan pertama dari w, kita cari titik stasionernya dengan menyamakan turunan pertama tersebut dengan nol, seperti berikut:
w’ = 2cos²θ – sin²θ = 0
2cos²θ = sin²θ
sinθ/cosθ = √2
tanθ = √2
θ ≈ 54,74°
Dari hasil di atas, maka nilai θ yang membuat fungsi w mencapai nilai maksimum adalah sekitar 54,74°.
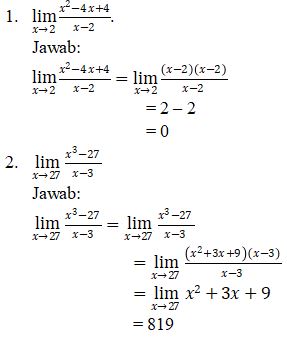
Contoh Soal dan Pembahasan Limit Fungsi Aljabar Tak Hingga untuk Memudahkan Belajar Matematika
Limit fungsi aljabar tak hingga termasuk salah satu konsep penting dalam ilmu matematika. Untuk itu, kita membutuhkan contoh soal dan pembahasan yang tepat agar dapat memahami konsep tersebut dengan baik. Berikut ini adalah contoh soal dan pembahasan limit fungsi aljabar tak hingga yang akan membantu kamu memahami konsep ini dengan lebih mudah.
Apa itu Limit Fungsi Aljabar Tak Hingga?
Limit fungsi aljabar tak hingga adalah upaya untuk menghitung nilai limit atau batas dari suatu fungsi ketika x mendekati nol atau tak terhingga. Limit fungsi ini memiliki nilai ketika ada dua garis yang saling berdekatan mendekati suatu titik, atau dalam istilah matematika, ketika jarak antara suatu angka dan angka limitnya mendekati nol.
Mengapa Penting untuk Belajar Limit Fungsi Aljabar Tak Hingga?
Limit fungsi aljabar tak hingga sangat penting dalam matematika, terutama dalam ilmu kalkulus. Limit berperan penting dalam penghitungan integral dan turunan. Limit juga digunakan dalam persamaan di segala bidang ilmu, seperti sebagai model dalam fisika, kimia, dan ekonomi.
Cara Menghitung Limit Fungsi Aljabar Tak Hingga
Untuk menghitung limit fungsi aljabar tak hingga, ada beberapa cara yang bisa kamu lakukan. Beberapa teknik di antaranya adalah sebagai berikut:
- Menggunakan aturan limit;
- Menggunakan teorema sandwich;
- Menggunakan penggantian variabel pada suatu fungsi.
Contoh Soal dan Pembahasan Limit Fungsi Aljabar Tak Hingga
Berikut ini adalah contoh soal dan pembahasan limit fungsi aljabar tak hingga yang akan mengasah kemampuan kamu dalam kalkulus.
Determinasi limit dari (7x-1) / (x-1), ketika x mendekati 1.
Pembahasan Soal
Dalam masalah ini, kita dapat menggunakan aturan limit bagi pecahan dengan mengganti x dengan nilai yang didekatkan dari kedua sisi sama. Ini akan menghilangkan ketidakterdefinisian fungsi karena x = 1.
Oleh karena itu, kita dapat menafsirkan pecahan [(7x-1) / (x-1)] sebagai berikut:
[(7x-1) / (x-1)] = [(7(x-1)+6) / (x-1)]
= [(7(x-1)/(x-1)) + (6/(x-1))]
= 7 + (6/(x-1))
Ketika nilai x mendekati 1, maka nilai dari u = x – 1 akan mendekati nol. Oleh karena itu, kita dapat menghitung nilai limit fungsi tersebut sebagai berikut:
Limit [7 + (6/(x-1))] ketika x mendekati 1
= Limit 7 ketika x mendekati 1 + Limit [(6/(x-1))] ketika x mendekati 1
= 7 + tak berhingga
= tak berhingga



